最近の機械学習はディープラーニングによって大いに発達し、様々な分野で精度の記録を更新する大躍進を起こしています。しかしその活躍も計算機の設計や多くの学習パラメータの調整にしわ寄せが行っているだけの話で、膨大な次元のデータがもたらす次元の呪いから逃れられたわけではありません。現に非常に高性能なコンピュータを使い、大量の訓練データを準備しなければほとんど性能は発揮されません。ビッグデータやIOTに代表されるように、インターネットの活用によって訓練データを集めることは容易になってきました。あとはいかにして大量のデータを処理するのかが過大だったのです。
しかし、ここでもう一度、本来高次元のデータがもたらしている次元の呪いについて再考したいと思います。計算機のパワーと様々な最適化の工夫によって隠れてはいますが、これがもたらしている影響は無視できません。
パラメータの数の爆発的増加
よく知られた事実です。回帰分析を行おうとした際に、入力データが高次元であればあるほど、推定しなければならないパラメータは増えていきます。
1次元多項式
仮に入力データが1次元である場合には、これを推定するには次数の数だけパラメータwを決定するだけで済みます(プラス定数項も)。
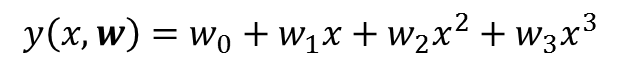
3次元多項式
一方で入力データが多次元である場合には、推定するパラメータwは爆発的に多くなり、仮に3次多項式で回帰分析を行おうとした場合には、入力データの次元がDであれば、Dの3乗のオーダーを持ちます(データの次元に対してべき乗で増加)。

指数的増加に比べればまだましですが、手に負えるものではありません。たった3次の多項式でフィッティングしようとしただけでも、入力データが2次元ならば約8個、3次元ならば約27個、4次元ならば約64個、5次元ならば約125個、10次元ならば約1000個……です。入力データが2桁や3桁なのは当たり前の世界なので、これはとんでもない数のパラメータを推定する必要が出てきます。
高次元確率密度、直感との相違
2次元のデータ
半径1の円の内部に、一様にデータ点が分布しているとしましょう。
ここで半径0.5の円で内側をくりぬくことを考えます。このとき、残った外側の部分にはどれだけの割合のデータ点があるでしょうか。

これは単純に面積の比を考えればよく、半径0.5の円の面積は、半径1の円の面積の0.25倍ですから、残された部分の面積はもともとの面積の0.75倍(75%)ということになります。
要するに2次元データが一様な分布で円形にプロットされたとすれば、半径の半分より外側に75%があるわけで、今後同種のデータも75%外側に現れると考えられます。くり抜く半径を一般的に1-εと置けば、残された青い部分の割合は以下で表されます。

これは何の疑問もありません。当たり前のことを言っています。
高次元のデータ
同様に高次元のデータを考えます(3次元であれば半径1の球状にデータが一様に分布しており、半径1-εの球で内側をくり抜くということです。4次元以降は図示をすることはできませんが、同様に高次元の半径1の球を1-εの球でくり抜くことを考えます)。
このとき、D次元球のくり抜かれた後に残った部分の割合(体積比)は

です。何のことはない、2次元のときの指数2をDに変えただけです。しかし、こんな当たり前のことですが、よくよく考えましょう。もしも1-εを0.9としましょう。つまり球の内側を(半径で見たら)ほとんどくり抜いてしまうということです。
しかし、0.9のD乗を計算する際にDが大きければ(データの次元が大きければ)0.9はほとんど0に収束してしまいます。
すなわち高次元データをプロットしたとして、球内に一様に分布するならば、データ点はほとんど球の表面にあるということになります。高次元になればなるほど、実は中身はスカスカなのです。(スカスカというのはおかしい。一様なのだから。でも高次元では半径の9割で球内をえぐりとってもほとんどデータ点が減らない!やっぱり中身はスカスカ!?)
ガウス分布の場合
しかし一様分布というのはあまり面白くありませんね。多次元ガウス分布の場合はどうなるのでしょうか。多次元ガウス分布の確率密度関数を極座標表示し、角度方向を積分して半径のみの関数とした場合以下となります。

つまり、p(r) を r1 から r2 まで積分すれば、高次元球の半径r1からr2までの薄球膜内(厚さr2-r1の薄膜内)にあるデータ点の数の割合が求まります。このp(r)は極大点を持っておりその値はDに依存し、極大点から離れると指数的にp(r)は減少します。以上のことから、多次元ガウス分布の場合は次元に応じて球の中心からある一定の半径の薄皮にほとんどのデータ点が集中していると言えます。
一様分布の場合には、外側ほど薄皮の体積が大きいために、最も外側の表面が大量のデータを抱えています(前述の通り半径の9割をくりぬいても、データ点はほとんど減らない)。
一方でガウス分布の場合は薄皮の体積は外側ほど大きいのは同じですが、データの散らばり具合(分散)とバランスが取れた部分にほとんどのデータが集中することになります。
当然1次元であれば中心が最も多く、2次元であっても中心から少しずれるだけです。高次元になると、中心にはほとんどデータ点はなく、中心から離れた特定の半径の薄皮上にデータ点が集中します。
次元の呪いに対して
見てきたように、低次元での直感は大抵高次元へそのまま一般化することはできません。しかし、低次元での考察が一切無駄というわけではありません。
高次元データの重要な変数は限られている
訓練データというのは一般的には高次元ですが、その中には殆ど知りたいことや予測したいことには関係ないデータも含まれるはずです。また、高次元とはいえど重要な変化をもたらすデータ空間の方向というのもある程度決まっているはずです。そのデータの方向が直線的であれば主成分分析によってデータの変化を説明する重要な方向を獲得できます。
高次元データは局所的には滑らかに変化する
入力データが少しだけ変化したとしても、得られる目標のデータには少ししか変化をもたらさないはずです。土地の広さ、間取り、駅からの距離、最寄り駅などのデータがあり、これから価格を決定しようとする場合に、土地の広さがほんの少し変わっただけで爆発的に価格が変化するようなことはないはずだということです。
そのようなことが全体で起こらないとは限りません。最寄り駅が非常に多くの路線を持っており、駅からの距離が徒歩10分を切るような地点で爆発的に価格が上がってくる場合もあるかもしれません(だとしても徒歩11分と10分で滑らかさがなくなるほど爆発的かは知りませんが)。しかしそういった点は例外のはずで、殆どの場所で滑らかであれば、その点以外を考えておいて、あとで繋げればいい話です。
ディープラーニングとの関連
ディープラーニングでは、データを大量に与えて時間を十分に掛ければ学習がどんどん進んでいくというように言われています。これは本来次元の呪いに嵌っている状態から、計算機のパワーによって高次元データに埋め込まれた局所的なデータの上手い方向を見つけているからだといわれています。
学習を進める上での評価関数が大量のパラメータによって極値に到達するには、パラメータに関するすべての偏微分の値がその点で0になり、かつヘッセ行列に対する条件も必要です。このような条件が偶然にも学習でピッタリ求まることは難しいはずです。学習が停滞しているのは高次元停留点(鞍点など)から脱出を図る最中であり、ディープラーニングの学習が停滞したように見えて、いつの間にか学習が進み始めるのはその脱出の方向を見つけるのに時間が掛かったからだといわれています。
二次元の停留点であれば、目でどちらに下がればいいのか分かりますが、これが高次元にもなり特定の方向にのみ下がれるようなケースでこれを探索するのは確かに時間が掛かりそうです(しかもちょっと進んだらすぐに下がれる方向は変わってしまうでしょう)。

囲碁ソフトGoAlphaは成果を挙げたものの、計算機に使われているパワーは非日常的ものです。次元の呪いを乗り越えるには今のところパワーを使うしかありません。ご飯を食べればそれだけで動く、エネルギーが有り余って太ってしまう人間とはやはりまだ原理的な部分が違うといわざるを得ません。
最適化を上手く進めるような手法の開発や、学習に力学系に関する研究も行われています。脳の模倣という生体の持つ不思議な力の応用と、数学という理論研究の言語を使って次元の呪いを乗り越える日がいつか来るのでしょうか。