最も単純な思想である最小二乗誤差推定があります。
これは多変量解析や機械学習でも最も最初に学ぶであろう内容です。次には過学習を防ぐために正則化を用いることを学ぶかと思います。
これらが、確率論の導入によって最尤推定とMAP推定に含まれることを見ていきます。数式は要点だけを見ていくので、詳しい式変形は追いません。しかしそれでも、近年統計的機械学習(確率論を使う機械学習の方法)が非常に活躍している理由が分かるかと思います。
SVMやニューラルネットなどの決定論的手法も確率的に取り扱えますが、なぜそんな面倒なことをやるのかを納得していただけたらと思います。
決定論的な多項式フィッティングの過学習対策
次数の問題
機械学習でモデルを得ようとする場合に、事前に設定しておかなければならない値があります。具体例としては、多項式を使ってフィッティングをしようとするとき、次数をいくつにするかという問題です。
データ点がM次の多項式
で近似できると考えた場合、真の曲線上の点に関して
を最小化する問題に帰着します。
つまり真の点から、点
との差の二乗和を最小にするような曲線
を獲得し、この曲線こそがデータ点を説明するものになっていてほしいのです。
この計算を実行する際には、の次数がいくつであるかは、予想して決めておかなければなりません。一次ならば、これを直線で表そうとしているということになります。はたしてデータ点が直線で表現できるものであるのか、それは誰にも分かりません。
仮に正弦波が真の曲線であり、ここから観測の誤差を含んだデータ点を獲得したとしましょう。これを多項式で表現しようとすると、次数は幾つにするのが良さそうかを見てみます。
以下は緑が真の曲線であり、青がデータ点、そして赤が最小二乗法により得られた曲線です。この場合は次数が3の場合にもっともまともな曲線が得られているように見えます。正弦波が一周期で2回ぐねっと曲がるため、これを上手く表現できそうなのは三次関数であろうというのは何となく分かることでしょう。
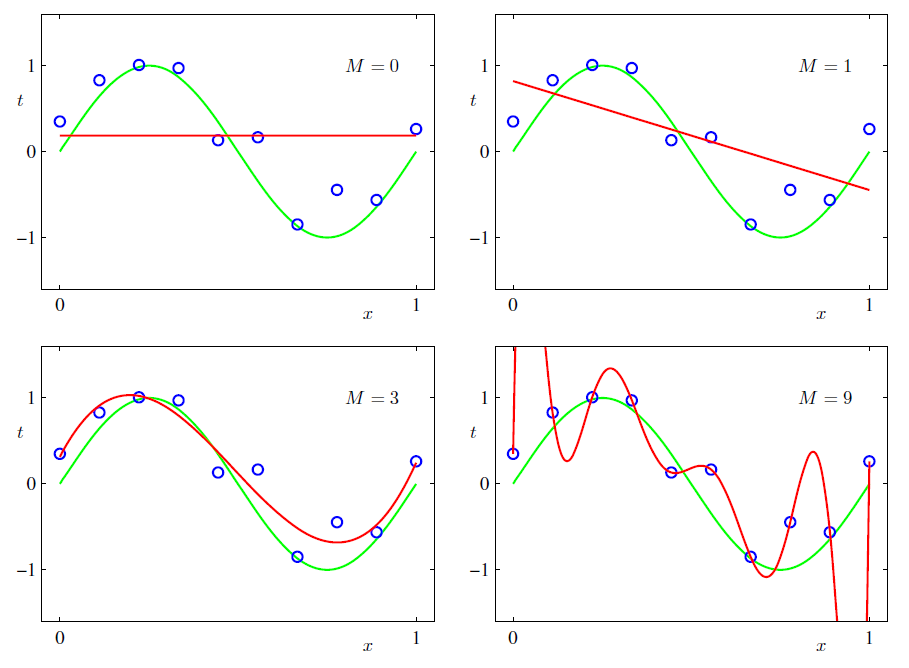
(参照:パターン認識と機械学習、C.M.Bishop)
しかし実際にデータを獲得した時には、元々の真の曲線なるものを知らないからこそ推定を行うのであって、次数が幾つだなんてのはハッキリ決まりません。もしも、正弦波であるという情報を知らずに、何となく次数M=9などと考えて最小二乗法を行えば、図右下のようなめちゃくちゃな曲線になっていしまいます。この曲線は、データ点をほぼ通過しているために、最小二乗法で最小化しようとしているは非常に小さな値になり、求めようとした数式の条件には合致しています。しかしそれはあくまでM=9だと仮定した上で合致しているのであって、M=9が正しくないのであれば、まともな結果は得られません。
このようにデータ点を上手く通過し、手持ちのデータのみを上手く説明できるようになったものの、本来の真の曲線を獲得できておらず、将来真の曲線から出てくるデータを説明できない状態を「過学習している」と言います。
この過学習を防ぐことは機械学習での大きなテーマの1つになっています。
過学習対策:正則化
過学習を防ぐ方法として正則化があります。
正則化とは、多項式フィッティングを行う際に以下のように最小化する関数を変更します。
↓↓↓
第二項に、余計な項が加わっています。この項を正則化項と言います。
本によってはペナルティー項などとも書かれており、要するに最小化を実行しようとしたときに、第一項だけを小さくできたとしても、第二項が大きくなるのはダメというペナルティーを与えて、wの値を考えなおさせることができるわけです。
普通に1つ目の式の最小化を実行すれば、M=9で推定した場合にひどい結果が得られてしまったのを見てきましたが、2つ目の式を最小化すれば、M=9という設定でもまともな曲線が獲得されています(下図)。
通常第二項は、本来フィッティングを行おうとした本質的な項とは無関係なため、λを非常に小さく取ります。下図左は、と設定されており、第二項はかなり小さな数です。しかし、この項を入れることで、単に二乗誤差を小さくする第一項だけでなく、やたらめったら大きなwの値を持たないように制限できるので、激しい変動は抑えられています。
もしものように、第一項と同程度の重要度を用いて最適化した場合には、あまりにも得られる関数は保守的になりすぎてしまい、ほとんど直線に近いものになります。

(参照:パターン認識と機械学習、C.M.Bishop)
正則化を用いると、次数はとりあえず大きめに取っておいて、正則化項を適当に変えてみることで過学習を解決することができます。次数の設定の場合、手当たりしだいにやってみなければならなかったところ、正則化を用いると、基本的にはλを小さい値で設定しておくだけで、ある程度まともなフィッティングを行ってくれます。
正則化項は、必ずしもでなければならないわけではなく、
などでも良いです。これは目的に応じて変える必要があります。それぞれの正則化項がどのような意味を持っているかは、正則化に関する詳しい解説に回します。現状はスパースコーディングと呼ばれる手法が主流となっています。
確率論的な多項式フィッティングの過学習対策
最尤推定によるフィッティング
真の曲線上に生じるはずのデータが、ガウスノイズに汚されていると考え、このガウスノイズの分散を計算することでデータ点がどのように生じているかを論じることができます。この場合、普通の多項式フィッティングと異なり、曲線を求めるだけでなく、データ点がずれてしまう過程を知ることができます。

しかし、これは本質的には普通に多項式フィッティングをした後に、得た多項式を真の分布と考えて手持ちのデータ点がどのように汚されたかを論じるのであって、得られる曲線自体は普通の多項式フィッティングと変わりません。重要なのは、データ点が得られる過程を論じることが出来るということです。
として、まずは普通のwを最尤推定で求めるのですが、最尤推定の推定式は以下の関数を最小化することに帰着されます。(実際には下記の式の負符号を最大化)
つまり、普通に多項式フィッティングをするのと変わりがありません。これは言い換えれば、最小二乗法という方法が、最尤推定と一致しており、統計学的に妥当な方法であるという裏付けになっているにすぎなく、前述の通り得られる曲線は同じになります。
wを求めたら、このwを既に決まった定数と考えて、残りの分散βを求めます。
この分散は、得た多項式からデータ点の標本分散の和を最小化するという、至って直感的に当たり前の結果によって得られます。
とにかく覚えておいて欲しいのは、最尤推定では普通の多項式フィッティングと得られる曲線は変わらず、よってwの次数Mの問題と過学習の問題は何も解決されていないということです。
MAP推定
今回の主題であるMAP推定です。ベイズの定理
を用いて、事後分布を最大化する問題にします。
(ベイズ理論が、パラメータwすらも確率変数だと扱っていることに注意してください。データDが得られたときにwの確率分布を扱います。)
最尤推定によって、と求められたとしましょう。
つまり得られる分布は以下のようになります。
これに対して、勝手に以下の事前分布を仮定します。
パラメータによって、
の分布はある程度こんなもんだろうと先に決めてしまうのです。当然のことながら、これが明らかにおかしいものであると上手く行かなくなります(この事前分布なるものの取り扱いでベイズ理論は嫌われていた)。今回の場合最尤推定の時点ガウス分布である仮定を用いていますから、ガウス分布に似たexpの含む分布を採用したということになります。
最大化しようとする事後分布は、最尤推定で求めた式✕事前分布÷定数であり、定数はどうでもいいので、結局、最尤推定で求めた式✕事前分布を最大化することになります。
最尤推定で求まる式自体は、MAP推定の時点では操作のしようがありませんので、結局は事前分布の設定によって最大化の式が変わるということになります。
この最大化の式は最終的には負符号を取り、以下の最小化の式に帰着します。
これは正則化付の多項式フィッティングの式
と酷似しています。β自体は既に求まっているもののはずなので、結局αの設定がλの設定に対応しており、事前分布の設定が正則化項そのものに対応していることになります。
まとめ

つまり役割としては、おおむね、最小二乗法と最尤推定は同じであり、正則化とMAP推定は同じであるということです。
確率論を用いるメリットとは?
結局得られる曲線は、それぞれの設定が同じであれば、全く同じものになるわけですから、わざわざ小難しい確率論を導入する意義がどこにあるのかを明確にしなければなりません。
1つは既に述べた通り、確率論の場合はデータがどのように汚されているのかという部分もモデル化することができます。今回の場合は分散○○のガウスノイズによって本来の曲線からデータがズレていると言えます。このノイズはたとえば化学の実験ならば計測装置の精度による観測誤差だったり、社会実験ならば個人差によるものだとかそういうことです。観測誤差やら、個人差なるものがどの程度あるのかを知ることができるのは、1つ有益ですし、逆に明らかに観測誤差を説明できないならば、フィッティングをやり直すという指標にもなります。
そしてもう1つが、MAP推定の場合は、MAP推定によってもとまった事後分布を、次回の事前分布に用いることができます。
という風にもとまったならば
とした
という扱いができることです。一度MAP推定したものは、恐らく適当に作ってしまう事前分布よりも信頼性のあるwに関する分布になっているはずです。データの計測が1日に数回しかできない場合は、1日でMAP推定をとりあえず終えてしまい、翌日のデータの事前分布として用いれば良いということになります。MAP推定で得られた事後分布に、1日目のデータの情報が含まれているわけですから、2日目は1日目のデータを加えて解析する必要はなく、単に2日目のデータに関して解析を行えばよく、1回1回の計算も楽になります。
別に1日おきでなくともよく、1時間毎でもいいですし、究極は1データごとでもいいはずです。普通このような学習の手法をオンライン学習と言います。オンライン学習の容易さは確率論(ベイズ理論)を用いる大きなモチベーションの1つです。