ノーフリーランチ定理というのを聞いたことがあるでしょうか。
汎用的な人工知能が研究される中、この定理についてもう一度見つめなおす意義は大きいと思います。ノーフリーランチ定理とは非常に簡単に言えば、全て問題に対して高性能なアルゴリズムは存在しないということを言っています。
(図:wikipediaより)
ノーフリーランチ定理とは
ノーフリーランチ定理は
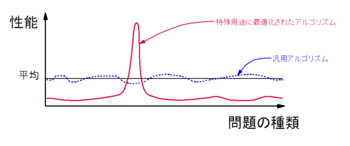
コスト関数の極値を探索するあらゆるアルゴリズムは、全ての可能なコスト関数に適用した結果を平均すると同じ性能となる
と説明されています。上の図がとてもわかり易く可視化されていますね。
メタヒューリスティックなアルゴリズムで色々な問題を解こうとすることへの反証として使われることが多いようです。つまり、問題が変わればアルゴリズムも変えるべきで、できる限り先見知識を使ってその問題に特化した解法を考案すべきということです。いくらデータ解析の手法が脚光を浴びて、高性能だと謳われたとしても、何でもかんでもそれに頼っていてはいけないということでしょう。
わかりきっていることはしっかり使おう
いま制約として1次の不等式や等式がある場合に、1次の評価関数を最適化したい場合にはどういう手法を考えればいいでしょうか。
などのケースです。数式を見れば、すぐさま制約条件から一変数を削除できることが分かりますね。を削除してしまえば評価関数は2変数の最適化問題であり、残りの不等式を使って、あとは
と
をどれくらいの配分で値をもたせればいいかを考えるだけです。こんな問題は非常に簡単なのでどうでもいいのですが、もっと変数が増えて、評価関数も複雑に見える(一見高次に見えたりする)場合には、すぐさま解法が浮かぶとは限りません。
この手の1次の式のみで構成された最適化問題を解く方法として線形計画法があります。
しかし、評価関数があり、それに対して制約条件があるといえば多くの人はラグランジュの未定定数法が浮かぶのではないでしょうか。ラグランジュの未定定数法は、制約条件の切る超平面上で評価関数が停留する点を探す一般的な手法です。
として元々の変数に対する偏微分係数=0とλでの偏微分係数=0が停留条件。
これは、制約条件の式における法線ベクトルと評価関数を等高線で表した際の等高線の法線ベクトルが線形従属であるという条件と同値であり、ラグランジュの未定定数はこの時の線形従属の関係を表す係数になっています。
法線ベクトルを求めるという作業は勾配ベクトルを求めるべく微分をしているわけですが、1次の問題に対しては勾配ベクトルなんてものは常に同じ方向を向いているに決まっているので、そんな作業をする必要なんて殆ど無いと分かるはずです。また、これは等式制約の話ですが、不等式制約があっても解けるような未定乗数法もあります。しかし、その理論はかなり込み入ったものになります(だって高次でも解けるような話をしているんだから)。
やはりこの手の問題ならば線形計画法で解いたほうが速いし精度も良いです。
複雑で難しい手法を使っていることに酔ってしまい、本来の目的を失うことは避けなければなりません。
ディープラーニングを応用する
ディープラーニングは脳の処理を真似て、自身で特徴抽出から学習までを一貫して行うようなアーキテクチャにすることができます(これは結果であって本質ではないですが)。またベイズ理論によってハイパーパラメータすらも学習によって推定できるような理論が出てきています。その便利さに溺れて、データを何でもかんでもディープラーニングに突っ込むのはどうなのでしょう。時間を掛ければ良い精度は出るかもしれません。でもそれってモット簡単に早く解ける方法あるかもしれませんよね。これはディープラーニングを応用するというよりは、ディープラーニングの解析評価や発展のためにデータが使われているような状況です。もちろんそういう研究も大事です。でも本当はデータのことを精度良く知ることが目的であれば、必ずしもディープラーニングが正解の手法ではないかもしれません。
ノーフリーランチ定理の注意点
こう言っていると汎用アルゴリズムの存在そのものを否定しているように見えますが、決してそうではありません。ノーフリーランチ定理は「全ての評価関数に対して、あらゆるアルゴリズムの平均性能が同じになる」と言っているのです。「全ての中の複数の評価関数に対して」ならばその範囲で汎用的に性能の出るアルゴリズムならば見つかるはずです。
ディープラーニングとひとえに言えど、CNNとDBNは全く異なるアルゴリズムです。
CNNは画像処理で非常に良い性能を発揮しています。これはCNNが空間的なデータに対して強いアルゴリズムだからです。これはちゃんと、画像というものにとって何が重要な情報なのかをしっかりと反映しています。
まとめ
結局、何が言いたいのかというと、人間が基本的な勉強をやめてはいけないということです。何かに対して解析をしようと思うのならば、その分野に対してちゃんと勉強しなければなりません。そこで得た知識がアルゴリズムに活かされて初めて性能の良い物になるのです。
初歩的なことから高度な内容まで、使いこなせるように基礎をおろそかにしてはなりませんという話でした。