既に深層学習は、chainerやtensorflowなどのフレームワークを通して誰の手にも届くようになっています。機械学習も深層学習も、あまりよくわからないが試してみたいなという人が数多くいるように思います。そして、実際に試している人たちもたくさん居るでしょう。
そんなときにぶち当たる壁は、多種多様なハイパーパラメータの設定です。
これはテストデータの精度に対して、試行錯誤を繰り返しながら決めていくしかありません。
しかし闇雲に値を変えて試してみてもあまり良い成果は得られないでしょう。
今回は、各ハイパーパラメータがそもそもどのような効果を持っているのかをまとめ、学習を行う際の指針になるようにしたいと思います。
ハイパーパラメータとは
ハイパーパラメータとは、簡単に言えば、学習を行う際に人間が予め設定しておかなければいけないパラメータのことです。ニューラルネットワークの結合の重みなどは、ニューラルネット自身が学習によって獲得するパラメータですが、ニューラルネットワークの層の数やユニットの数、正則化の係数などは人間が予め決めておかなければなりません。
これらハイパーパラメータの設定によって学習の結果が大きく左右されることは、深層学習をやっている人ならばよく知っていることでしょう。
今回はそれぞれのハイパーパラメータが学習にどのような影響を及ぼしうるのかをまとめます。
ユニットの数をどうするべきか
入力層のユニットの数は、データの次元に一致させる必要がありますから迷うことはありません。そして出力層のユニットの数も、分類したクラスの数だけ準備するので考える必要はないです。
では中間層のユニットの数はどうすればいいでしょうか。入力のユニットの数よりも増やすべきか減らすべきか。これらは一概にどっちが良いとは言えない問題になっています。
中間層のユニットの数を膨大にする
実は、入力層と出力層の間に、たった1つの中間層を準備するだけで理論上は十分なのです。そのためにするべきことは「中間層のユニットの数を限りなく増やす」ことです。
中間層のユニットが限りなく多いとき、任意の関数が近似できることが知られています。すなわち、解きたい問題に対する如何なる分離超平面も表現することが可能なのです。
ただし、学習で与えるのはあくまで訓練データです。訓練データを完全に分類できるようにニューラルネットを学習させたところで、汎化性能が良いとは限りません。ただ、ここで知っておくべきことは、ユニットの数は多ければ多いほど、ニューラルネットの表現できる関数の幅が広がるという事実です。
中間層のユニットの数を少なくする
入力層よりも中間層のユニットを少なくするというのは、データを表現する次元は、本来はもっと少ないはずであると考えていることになります。入力データのある成分が「冗長である」と考えているのです。実際多くのデータは、手当たりしだいにかき集められたものであって、これから分類しようと思っていることに対して有効な手がかりになるのはごく一部でしょう。
例えば人間が他人の表情を見て笑顔であると判断するとき、顔の隅から隅まで見ているわけではありません。口とか目元とかの変化だけで分類が出来るはずです。
結局どちらが良いのか
従来の機械学習の場合は、手元のデータの次元を落とすことで、データの本質的な部分を抽出しようと試みてきました。そういう視点に立てば、中間層は本来絞られるべきです。
しかし、現在のニューラルネットは計算機の性能向上と、最適化アルゴリズムの工夫によって中間層が多くても学習がしっかり進むようになっています。あえて冗長な表現力を持たせておき、学習の過程でニューラルネット自身に判断を委ねるのです。
したがって、迷うのであればユニットの数は学習に掛かる時間を考慮しながら、取り敢えずは多く設定しておけばいいでしょう。当然、それよりも少ないユニットで同じ精度を出せるのであれば、学習の手間を考えても明らかに後者のほうが良いです。しかし、それがどの程度の数なのかは知るよしも無いのです。
ニューラルネット自身に判断を委ねるためには、冗長な表現力によって過学習が起こらないように学習を制御してやらねばなりません。これにより、更に多くのハイパーパラメータが必要となってきます。
荷重減衰
荷重減衰の効果
荷重減衰は、ニューラルネットの重みパラメータに対して、
が大きくなり過ぎないように制約を与えます。ハイパーパラメータとしては、荷重減衰をどれほど重要視するかを指定する係数を決める必要があります。
この制約がどのような効果を持つのかを簡単な図で説明します。
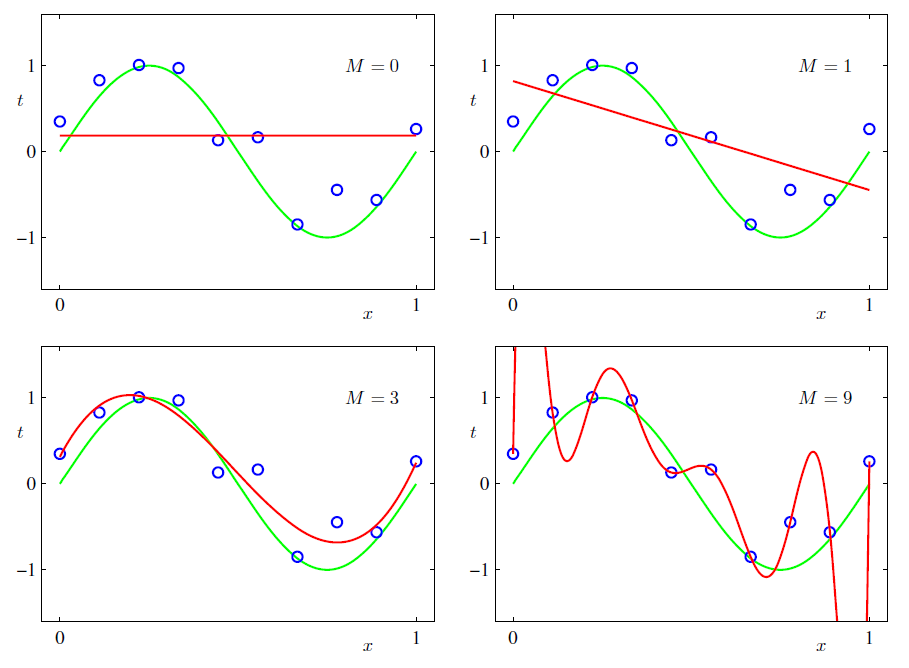
以下はPRMLの3章に載っている多項式フィッティングの図です。
赤い線が学習で得られた曲線。緑が本来の正しい曲線。青丸がデータ点です。
図中のという値は、多項式の次数です。これはニューラルネットで言うところのユニットの数とでも言えるでしょう。これが多ければ多いほど複雑な形を表現できます。しかし、悪戯に多くしてしまうと、図右下のようなデータにだけ無理やり帳尻合わせをした結果が得られてしまいます。しかし通常、データが本来どのような形をしているかは分かりません(わからないからこそ学習する)。ですから左下のように都合よく
と設定して上手く行くなんてことはめったにありません。
先ほど述べたように、ユニットの数は通常多めに設定しておきますが、するとニューラルネットは高い表現力のあまりデータにだけフィットする過学習に陥ってしまいます。
そこで用いるのが荷重減衰です。
荷重減衰を用いると、表現力の高いモデルを仮定していたとしても、その学習は抑制され、丁度いい具合に落ち着かせることができます(図左)。
しかし逆に荷重減衰を強くし過ぎると、学習はほとんど進まなくなります(図右)。
回帰でも分類でも基本的には同じです。目的関数の違いだけであって、ニューラルネットはあくまでを最適化しようとしています。その最適化される
の大きさに制限を与えることで表現力を抑制するのが荷重減衰です。
荷重減衰の注意点
荷重減衰を大きくし過ぎると学習を抑制しすぎてしまい、逆に小さすぎると自由にさせすぎてしまうことが分かりました。しかし、荷重減衰のハイパーパラメータは実は厄介な性質を持っています。
それは、まったく同じ構造のニューラルネットを準備して、まったく同じ分類問題を学習させるとしても、入力値のスケールが変化するならば調整しなおさねばならないということです。
荷重減衰というのは、入力データの値に対して相対的に決められるべきものなのです。
無論、分類問題が変わると、荷重減衰のハイパーパラメータの具合は完全に変化します。
通常の正則化であれば、あくまでモデルに対して上手く制約を与えるのですが、荷重減衰の場合はデータ依存であるということを把握しておいてください。
スパース正則化
スパース正則化の効果
スパース正則化は、ユニットの活性の割合をコントロールする正則化手法です。
こちらは重みに直接制限を与えるのではなく、指定した割合しかユニットが活性しないような重みになるように学習を進ませます。こんなことをするのは、データに対して冗長なユニットを準備しているという前提があるからです。
仮に入力データの次元よりも遥かに少ないユニット数の中間層を準備したにも関わらず、この正則化を入れてしまった場合は、ニューラルネットは更に少ないユニットでデータを表現しようとしてしまい学習が上手く行かなくなる可能性があります。
ハイパーパラメータとしては、スパース正則化をどれくらい重要視するかを決める係数と、活性の割合を設定することになります。
スパース正則化の発想
この正則化は荷重減衰と異なり、学習するパラメータを直接制御しようとするものではありません。データに対して冗長なユニットを準備しているので、一部しか活性しないように学習をさせるのですが、人間が勝手に数を減らすのとは違い、学習を進めながら損失関数を減少させつつ活性の割合をニューラルネット自身が調整していくことになります。
つまり、指定しているのは活性の割合だけなので、学習の途中で「やっぱりこっちのユニットを活性させて、あっちを非活性にしよう」という判断を委ねることが出来るのです。これはただ単に最初からユニットを少なくしておくのとは全然違います。
ドロップアウト
ドロップアウトの効果
ドロップアウトは学習を始める際に、一部のユニットをある割合で非活性にしてしまう方法です。スパース正則化と何が違うのかというと、一度非活性だと決められたユニットは、学習そのものに参加しないのです。ハイパーパラメータはドロップアウトさせるユニットの割合です。
スパース正則化では活性の割合を人間が決め、全てのユニットを学習には参加させつつ、どれを非活性にするのかはニューラルネットが決めていきます。
一方ドロップアウトでは、一部のユニットを非活性にすることで、ネットワークの制限された構造だけで学習を進めていきます。そしてドロップアウトの対象を選出しなおしては再び学習を再開するということを繰り返していくのです。これは準備したユニットの一部だけを使って学習したニューラルネットが、あたかも複数個あるかのようです。
すなわち、準備したネットワークの一部を使って学習するというのを、少しずつ構造を変えながら進めていき、予測を行う際にはそれら複数の構造が協調しあって1つの結論を出すのです。
強力な正則化
ドロップアウトに選ばれたユニットは一切学習には参加しません。したがって、ネットワークの表現力を強く制限することとなり、かなり強力な正則化の効能を発揮します。
以下の図で言えば、ドロップアウトはの数を極端に少なくしていることになります。
荷重減衰がユニットを多く準備しつつ、重みに制限を掛けていたのに対して、こちらは直接ネットワークの自由度を制限するという方針だと言えます。
学習率
学習の決め手
学習率は勾配法によってどれだけ大きくパラメータの更新を行うかを決めるハイパーパラメータです。学習率、あるいはその勾配の算出方法に関する工夫は様々提案されています。
基本的に、学習率はいつでも一定にするのではなく、学習が進む毎に変化させるべきです。
特に通常は、学習が進むに連れて小さくしていきます。
論文でも酷い場合は一定、あるいは学習が進んだら10分の1にするなどという設定がされていますが、学習率は学習を大きく左右する重要なハイパーパラメータです。
必ず時間的に変化させる工夫をしなければなりません。
特に確率的勾配降下法やミニバッチ法を使う場合は、データによって損失関数の形状が変わりますから、今使われているデータでは損失が低下する更新だとしても、全体では上昇するような場合もあるのです(これがデータの冗長性を上手く活用できる理由にもなりますが)。そのような不安定な学習方法を使う場合は、学習後期段階では更新量を小さくして収束へ向かわさなければいけません。
オプティマイザー
なぜたくさんの種類があるのか
モメンタム法やAdaGradに始まり、AdaDelta、RMSProp、Adamなど様々なオプティマイザーが登場してきました。学習の基本は勾配法です。勾配を計算して下っていけばいいだけのはずです。
しかし、勾配が平坦なところにたどり着くと学習はしばらく停滞します。しかしそれで学習を止めずに根気強く待っていると再び学習が再開されるという現象が起こるのです。この現象から速く抜け出すようにするためには、単に勾配を計算するだけはダメだということが認識されるようになり、様々なオプティマイザーが提案されてきました。
学習の停滞が再び再開される理由
実は、勾配法の場合ローカルミニマムで学習が終わるのですが、ニューラルネットの学習ではそれはあまり問題ではありません。精度が高ければローカルミニマムだろうと構わないのです。問題は質のいいローカルミニマムに辿り着くまでにたくさんの鞍点や特異点があることです。
オプティマイザーはどれを選ぶべきか
これは結論を申し上げると、試すしかありません。
なぜなら、元々経験則で構築されたものであって、理論的根拠は乏しいからです。
一応、なぜそのような計算方法が提案されたかの背景を説明します。
・モーメンタム
モーメンタムは、現在の勾配と一つ前の勾配の重み付き和で更新方向を決定します。
1つ前の勾配方向の影響を受けながら現在の勾配方向にも進むということです。すなわち学習する際のパラメータの移動に慣性を持たせます。
・AdaGrad
学習が停滞するときは、その場所の勾配通りに進んでいては中々抜け出せないということです。たいていは同じ勾配方向にゆっくり進むことを続けていることが想定できます。そこで、同じ勾配方向ばかりが現れた場合は、その方向に対する進みを減衰させ、出現頻度の少ない勾配方向の成分を優先する計算を行います。
具体的には過去の勾配を全て考慮して、その二乗和の平方根で割ってしまうのです。
・AdaDelta、RMSProp
AdaGradの場合は、同じ勾配方向の成分が出続けた場合、その成分を減衰させすぎるために、本当にその方向に行かなければならないときに収束が遅くなることが予想できます。
そこで、過去の勾配全ての情報を均等に扱うのではなく、古い勾配情報ほど考慮する度合いを低くしていきます。すると過去に使った勾配だからという理由だけで、その方向を減衰させるようなことはなくなり、できるだけ側近の情報だけで上手く方向を修正するようになります。
・Adam
AdaDeltaなどのように新しい情報ほど優先する機能をそのままに、それを勾配方向の成分の大きさだけでなく、勾配そのものにも用います。モメンタム法と組みあわせたような形です。
当然モメンタム法に相当する部分にも過去の情報を新しい方から優先して計算に取り込みます。
ご覧の通り、どれが上手く行きそうなのかは分かりません。極端な話、凸最適化問題ならば普通に従来的供されてきた方法のほうが速いに決まっています。
ニューラルネットは損失関数が複雑な形状をしていることが予測できるので、様々な工夫がありますが、実際それのうちどれがどのように働いているかを完璧に把握するすべはありません。
以下は更に詳しい話です。
ディープラーニング関連の様々なパラメータについて更に知りたい方は以下