ニューラルネットワーク
ニューラルネットワークとは機械学習の立場から言えば、線型結合と非線形変換を繰り返す合成関数です。合成関数のパラメータ
をうまいこと調整することで、入力
に対して望む出力を獲得することができます。
もともとこれは、脳のモデルとして考案されたもので、これが万能的な学習能力を持っているとして脚光を浴びました。
脳のモデルとしての構造
視覚における神経細胞モデルとしてはネオコグニトロンが有名で、これは現在使われている畳み込みニューラルネットワークの前身とも言えます。
脳のモデルとしてニューラルネットを見る場合、入力層に相当するものは感覚層と表現できます。例えば視覚で言えば網膜などがそれに相当するでしょう。光を入力し、私達はその入力に応じて書いてある文字が何であるかを認識できます。その認識を行う出力層は判別層と表現できます。そして中間層に当たる部分が、何らかの情報の処理を行っている部分で連合層と呼ばれます。この連合層がうまい特徴抽出を行っている部分だと言えます。
図で言えば、コントラスト抽出から高次特徴抽出までが連合層という具合です。
連合層(中間層)の役割とは
単純パーセプトロンには連合層に相当する部分はありません。入力を適当に線型結合し、その値が正であるか負であるかで判別を行います。
つまり入力ベクトルの場合には、
という値の正負のみを見ているのであって、どんなうまいや
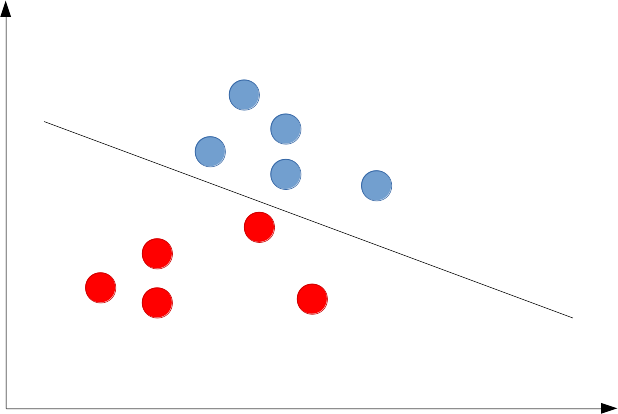
を設定しても以下のように線形分離しか行うことができません。
(線形分離可能)
(線形分離不可能)
これでは応用上非常に苦しいモデルとなってしまうだけでなく、我々の目がまさかそんな単純な判別しかできないとは思えません。そこで連合層(中間層に相当するもの)というものが良い働きをするのではないかと考えることができます。
入力ベクトルの場合には、
という値を考えます。とすれば、上記で得られる
種類の
が次の層(連合層)の
個のニューロンにそれぞれに入力されるという具合です。ニューロンは活性化
を行い、
という値を出力します。この出力を使ってもう一度線形分離に相当する判別を行うのです。
ここで重要なのは、一般に入力層の次元と出力層の次元
に関しては
であるということです。今、
次元の入力では線形分離ができなかったような場合にも、中間層(連合層)を考えることでそれが可能になるような表現の獲得を望んでいるんのです。それがなぜ次元を上げることと関係があるのかを以下の図で見てみましょう。
2次元の入力データは線形分離が不可能である。
これを以下のように上手く3次元に変換する。
するとデータ平面を差しこめば分離できる。すなわち線形分離可能になる。
このように上手い入力データの変換を獲得できさえすれば、それを新たな入力だと思って線形分離を行えばいいということです。通常、もっとデータが混ざり合っているような入力だとしても、それに応じて次元を十分にあげてやれば、線形分離が可能になるような変換は必ず存在します。
そのような良い変換を獲得するのが中間層(連合層)の役割だと言えます。
ニューラルネットの特徴抽出
このような分離を助ける特徴抽出を人手で行う場合は、通常次元を削減することを行うかと思います。主成分分析でも線形判別分析でも、統計的な手法の多くはデータの良い部分空間を求めるのが目的となっています。ニューラルネットの考え方はしばしば、このような特徴抽出の概念と逆行しているように見えるかもしれません。
それはやはり、ニューラルネットが元々は脳のモデルという体を持っているからだと思います。
すなわち、従来の特徴抽出手法は、人間がデータを可視化する際に3次元や2次元に落としたいとか、データ処理が楽になるように次元を落としたいなどの都合も含まれているわけです。無論、大量のデータの中から本質的に重要な情報だけを集めたいのならば、次元削減というのは有用な手法になりえます。
しかしニューラルネットが特徴抽出をするという場合には、可視化できるとか、データの意味を探ることができるとかはあまり要件には含まれません。
脳の細胞に電極が差し込まれ、活動を調べたときにデータの次元が少なくて済むには、連合層のユニット(ニューロン)の活動は少ないほうが良いに決まっているのですが、そうなるように活動しようなどと、神経細胞たちが考えているわけではありません。きっと対象を処理できるようにフルで活動します。あくまで、判別を行う際に脳にとって区別が付けられるような表現を獲得するのが目的です。
従ってニューラルネットで言うところの特徴抽出というのは、基本的には判別に(なんだかよくわからないが)有利になるような表現を獲得するということです。
そして、その特徴抽出(連合層の調節)も誤差逆伝搬法により識別が上手く行くかを見ながら学習ができるため、非常に汎用性の高い機械学習手法となっています。
実際には主成分分析などの次元削減で、学習とは一切関係ないノイズに相当する成分を切り落とせるのであれば、それは積極的に使っていったほうがいいでしょう。その後、次元削減したデータをニューラルネットの学習データに使えばいいのです。
実際にはその程度で落とせるノイズは、ニューラルネットが学習の過程で自身で落とせます。
例えば自己符号化器は主成分分析と同等の活躍をできます。自己符号化器を以下で構成し、更にこれを多層化すれば当然、主成分分析よりも複雑な特徴抽出が行えます。
ニューラルネットで次元削減を行う層を(1つ)作る
こうして特徴抽出器を構築した後、これを新たな入力と見立てて層を何層か追加(連合層と出力層を追加)し、全体で誤差逆伝搬学習を行うのです。
この場合連合層の識別に有利な特徴抽出が学習されるだけでなく、次元削減に相当する特徴抽出自体も学習の過程で再度最適化することになります。
実際には表現力の高さはすさまじいですが、それに伴ってパラメータも膨大であるため、問題に応じては従来の手法を用いることも検討すべきでしょう。
ただ、万能学習機械としての可能性を秘めているということは確かです。
ニューラルネットワークは本質的に教師あり学習
ご存知の通り、ニューラルネットは出力と正解を見比べて、ダメならば自身のパラメータを修正していく方法で学習を進めます。誤差逆伝搬法と呼ばれるとおり、自身の出力と正解を見比べた際の誤差が、出力側から計算され、順番に前の層にどれくらいパラメータを修正すれば辻褄が合いそうかを渡していきますから、そもそも誤差なるものを計算できなければ学習はできません。
ニューラルネットに詳しい方ならば、教師なしのニューラルネットがあることを知っているかと思います。しかし、あれは本来の目的である「正解ラベル」を与えていないという意味で教師がなしと言っているのであって、誤差を計算する際にニューラルネットに出力してほしい目標値が無いというわけではありません。
例えば自己符号化器ならば、入力自信が目標値になります。つまり、入力データが教師データとなっている教師あり学習なのです。
そして、脳のことを考えたときには、必ずしも「こうなるべきだ!」というような教師データがいつでもあるとは考えられません。つまり、ニューラルネットの学習は脳の活動のほんの一部を表しているのであって、これが全てとは全く言えないのです。
例えばスキーやスノーボードでは、転べば何かが間違っていたと理解できます。
しかし、何が間違っていて、どうすれば良いのかというのは分かりません。ただただ「ダメだった」ということしか分からないのです。同様に「できた」という状態が訪れても、何が良かったのかははっきり分かりません。いわゆる「慣れ」が訪れるまで練習を重ねなければいけないのです。
このようなケースでニューラルネットの学習は無力です。
強化学習
囲碁で人間を打ち破ったAlphaGoは強化学習を用いています。
時代ですから同時にディープラーニングも応用されていますが、実際には強化学習の「教師を明確に持っていなくても学習ができる」という構造がなければこの成果は得られなかったでしょう。
強化学習の概要
スキーを例に取れば、エージェントとはスキーをしている人です。環境はスキー場なり何なり周りのことを言います。
いま滑る際に何らかの行動を人間が取れば、環境には変化が及びます。スキー板で押されて雪が沈み、スピードが上がっていくかもしれません。止まろうという行動ならば、雪を跳ね飛ばし、その摩擦力で減速していくでしょう。その具合を観測しながら自分の状態を認識し、人間は自信の微妙なコントロールを行っています。
ところで初心者ならば、転んだり、思い通りに止まったり曲がったりできないということが出てくるはずです。しかし、膝の曲げ具合がどれくらい悪かったのか、上体の角度が良くなかったのか、明確な正解からの誤差なんてものは一切わかりません。分かるのは、転んでしまったから悪かったのだろうということだけです。これが環境からエージェントへの報酬に相当します。
そして人間は環境からの報酬を受け取り、環境を観測しながら行動を決定していき、試行錯誤しながら上手く滑る方法を体得して行きます。この過程を再現するのが強化学習です。
Q学習
強化学習の代表例であるQ学習を見てみましょう。
これは以下のようにを更新していきます。
まずというのは時刻
における状態(state)です。そして
は行動(action)になります。
というのは、状態
において行動
を選択した場合の価値です。
この価値が上手く求まりさえすれば、あとは価値を最大にするような行動を選べばいいわけですが(かなり乱暴ですが)、実際には明確な教師がないため価値の具体的な形は分かりません(教師ありならば、誤差関数というものが予め定義され最小化すべきものが明示的にある)。
したがって、環境から得られる報酬などを考慮して、そもそも価値とは何なのか自体を知っていかなければなりません。
その価値関数の探り方が上記の式で表されるのですが、これは最適制御理論など機械学習とは少し違った分野で発達してきた経緯があるため多くの機械学習の本では詳しく解説されていません。
強化学習の本としては有名なものに以下のものがあります。

- 作者: Richard S.Sutton,Andrew G.Barto,三上貞芳,皆川雅章
- 出版社/メーカー: 森北出版
- 発売日: 2000/12/01
- メディア: 単行本(ソフトカバー)
- 購入: 5人 クリック: 76回
- この商品を含むブログ (29件) を見る
最近出版されたものでは(私はまだ手に取っていませんが)以下があります。

- 作者: 牧野貴樹,澁谷長史,白川真一,浅田稔,麻生英樹,荒井幸代,飯間等,伊藤真,大倉和博,黒江康明,杉本徳和,坪井祐太,銅谷賢治,前田新一,松井藤五郎,南泰浩,宮崎和光,目黒豊美,森村哲郎,森本淳,保田俊行,吉本潤一郎
- 出版社/メーカー: 森北出版
- 発売日: 2016/10/27
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (1件) を見る
深層強化学習:Deep Q Network
深層強化学習では、この価値の推定に深層学習が導入されています。
ニューラルネットは本質的に教師あり学習ですから、を予測するために何らかの教師を設定しなければなりません。その方法は自体は割と従来から知られていましたので、新規性は単に、価値の予測に畳み込みニューラルネットを用いたところにあると言えます。つまりベースは従来の強化学習でありだからこそ本質的に強化学習の力を再認識すべきだと言えます。
脳との関連
大脳基底核で発生するドーパミンに着目しましょう。
例えば、ある動物が行動Aをやって行動Bをし、その後行動Cを経た場合にはエサをもらえるとしましょう。仮に行動Cだけを行ってもエサはもらえません。自動販売機とまでは行きませんが、ある動作を順番に行ってようやく食べ物が出てくるような機械を想定すればいいです。
運良く、A⇛B⇛Cの順に行動したときにエサが出てきました。そのときに動物の脳内でドーパミンが出ます。
しかし、エサをもらう過程を上手く学習していくと、次第に行動Bの時点でドーパミンが発生するようになります。更に進むと行動Aの時点でドーパミンが出ます。学習が進み、もはや機械のからくりを完全に把握したため、試行錯誤することなくその動作が最善だと分かるようになったのです。
ドーパミンは強化学習の報酬に対応します。
強化学習は大脳基底核のモデルになると言われており、脳のモデルとの対応関係を示す研究も盛んです。
特に脳のモデルを明らかにし、それを参考に新たな機械学習手法を提案するような動き、あるいは脳のように汎用的に情報処理が行える汎用人工知能の研究も行われています。
その他
連想記憶ネットワーク
物理的なモデルとしてはホップフィールドネットワークとして知られています。
ボルツマンマシンとも関連が深く理論的に面白いモデルです。
自己組織化マップ
(自己符号化器などと異なり純粋に)教師なしで、入力を任意の次元へ写像します。機械学習の手法として(おそらく)多様体学習に相当してくるかと思います。
ニューラルオシレータ
興奮と抑制の両方を使い信号を制御し、歩行や走行など様々な状態(リズムが違ったりなど)の遷移を調節します。
例えば、歩行と走行では足の動かすリズムは異なりますが、これを完全に別物としてではなくニューラルオシレータで制御することで、ロボットの動作を入力に応じて動的に遷移させることが可能になり、そのような研究例があります。