はじめに
機械学習での学習とは、パラメータを逐次最適化することです。
最適化数学自体は、それだけで1つの広大な研究範囲を持っていますが、今回は機械学習で用いられる逐次最適化が分かるように、最適化数学の基本を記したいと思います。
機械学習には非常に多くの手法がありますが、逐次最適化という面においてはほとんど共通の形を持っています。各手法毎に最初から理解のし直しが必要というわけではなく、最適化数学の基本を抑えておけば、新しい手法を学ぶときにもやっていることを理解することが可能になります。
最適化数学
最適化数学とは、目的関数を最大化したり最小化したりする手法を扱う分野です。
機械学習においては、目的関数として二乗誤差関数や交差エントロピーなどが用いられますが、その形によらず、最適化の着目する部分というのは共通しています。
したがって、目的関数の形に捕われず、最適化数学の狙いというものをここで理解しておきましょう。
ちなみに、同じ最適化手法を使っていたとしても、目的関数を色々変えることで機械学習としては異なる手法の名で呼ばれることとなります。
最適化問題の簡単な例
最適化問題とは、あるパラメータ制約のもとで、ある関数の最大値や最小値、そしてそのパラメータを求める問題です。例題を見ましょう。
上の式が目的関数です。下の式が制約と呼ばれるものです。
目的関数を見れば、この式を最大化するためにはか
のいずれかが負の値で、もう一方が正の値であればよく、そしてなるべく絶対値は大きければ良いと分かるでしょう。
しかし、自由にや
を選べるわけではありません。制約の式を満たしておく必要があります。
例題の解法
このような問題ならば非常に簡単に解けます。制約の式から、以下の関係が成り立たねばなりません。
今から目的関数の数値をいろいろ変えてみようという場合には、この制約の下で動かすことしか考えないため、この式を目的関数に代入してしまいましょう。
私達が最大化しなければいけないのは、このです。
は消えてしまいましたが、この目的関数を最大化するような
を求めた後に、制約の式から
を求めることができます。
この問題は簡単に解けて、高校数学が分かれば平方完成をしようと考えますし、微分で極値を求めるということもできます。
平方完成ならば
と変形して、のときに最大値
と求まります。一応
も求めると、制約式から
と求まります。よって最大値は、そのときのパラメータは
です。
微分で解こうという場合にはを
で微分することを考えます。極値は微分が
となる点ですから、
とすぐさま求まります。この値をに代入して同じように最大値と
を求めることができます。
微分による解法の注意点
今、微分によって最大値を求めることができたのは偶然です。
微分は極値を求めることができるだけで、それが最大値であるのか最小値であるのか、はたまたそのどちらでもないのかは分かりません。微分がの点は、そこから微小だけ動いても大きさが変わらない場所であるということしか言えません。
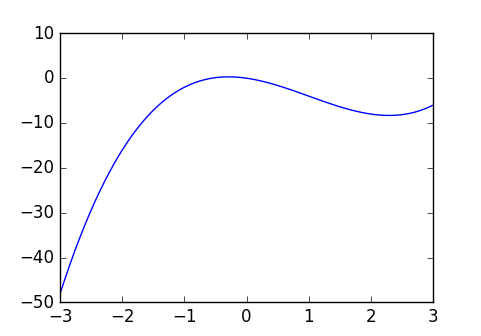
の点で微分が
となるが、最小値でも最大値でもない
通常、微分しての点が複数出てくるはずです。そのときはその全ての点での関数値を調べて、最小値や最大値を探す必要が出てきます。また、制約条件の端っこの点において、値が最小や最大となるケースもあるので、意外と見つけるのは難しいのです。
微分が
となる点が複数(2つ)ある例。
の範囲において、最小値は
の点であり微分は
でない
しかし、最適化数学ではこの微分を多用します。
先程の例では平方完成による方法で、確実に最大値を求めることができましたが、通常の関数ではそのような上手い方法が存在しないことのほうが多いです。なので微分に頼る他ありません。
凸最適化問題
凸関数
では、なぜ先ほどの例では微分で上手く解が求められたのでしょうか。
それは、先ほどの問題が「凸最適化問題」と呼ばれるものの一種であったためです。
凸最適化問題というのは、目的関数が凸関数であるような問題です。
この問題においては微分してになる点がたった1つしか求まりません。その点は最大値か最小値のどちらかであることが保証されます。関数の形を考えれば、それが最大であるか最小であるかは見当がつきますし、つかなかったとしても、極値での関数の値と、他の適当な点での値を比較すれば、最大であるのか最小であるのかはすぐに分かります。
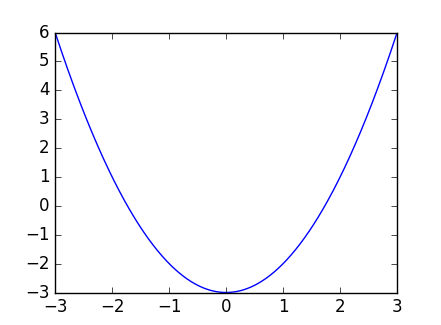
凸関数の例として簡単な例はのようなものです。
や
なども凸関数です。
簡単に言えばプロットしたときに山が1つ(あるいは谷が1つ)という形をしているタイプのものを言います。これは当然、微分してになるところが1つに決まっていますし、そこが最大値あるいは最小値になっているのも納得でしょう。
しかし変数が増えて、プロットする次元が増えていけばもはや目で確認するのは不可能です。
それに対して数学的に定義をすることで、式変形のみで凸関数というものを論じることができます。
ちなみに上記のは下に凸の関数、あるいは単に凸関数と言います。
反対向きに山があるタイプの関数は上に凸の関数、あるいは単に凹関数と言います。
凹凸の文字から連想するのと、関数の形が逆じゃないかと思うかもしれませんが、そのように定義されているので勘弁してください。分かりづらければ、上に凸とか下に凸と言うと良いでしょう。
ちなみになぜそのように名付けられるのかは、2階微分の値に由来します。
凸関数の定義
多変数の関数を表したい場合、
と変数を格納するベクトルを書いておいて、
と表記することにします(これはいろんな教科書でもそうする場合が多いです)。
関数が(下に)凸関数であるとき、任意の異なる点
と、スカラー値
を用いて、以下が成り立ちます。
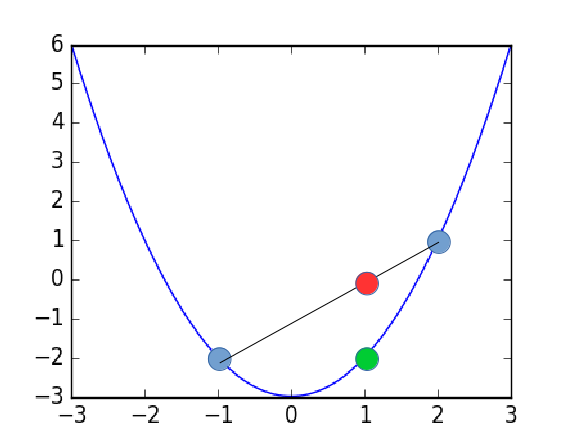
式の意味が分かるでしょうか。
青い点が、
での関数
赤い点が右辺に対応、青い点の線分上の点
緑の点が左辺に対応、青い点
の間での関数の値
一変数でもしっかり下に凸な関数の性質を表せており、多変数に拡張して、多次元でプロットしても同じことが言えます。従って、関数の凸性を上の式で定めてしまえば後々便利になります。
通常最適化問題の理論というのは、この凸関数に対して如何に効率の良い解法を見出すかと、非凸な関数が目的関数になってしまったときに、それをなんとか変形して凸最適化問題に帰着できないかに費やされます。
非凸に対して一般的に最大値や最小値を綺麗に求める方法はないため、大域的アルゴリズムの研究も盛んです。(例えば遺伝的アルゴリズムや粒子群最適化などが有名)
ともかく、目的関数を見たときに、それが凸であるのかどうかというのが重要であることはわかったと思います。
もしも最小化問題を解きたい場合には、目的関数が凸関数であれば、解くのが速いかはさておいて、ある点から適当に初めて、少しずつ今の場所よりも関数の値が下がっていく方へ移動していくという単純な方法が使えます。いつか点を動かしても関数の値が変化しなくなるはずですから、その点が確実に目的の最小解になっています。
この基本的なアイデアが、勾配降下法とか最急降下法などと呼ばれている手法です。
これはニューラルネットワークにしても何にしても、真っ先に思い浮かぶ解法で、機械学習にとって最も重要かつ、頻出の手法です。
ニューラルネットの学習
ニューラルネットの目的関数
ニューラルネットワークとは、簡単に言えば以下のような関数の形をしています。
そして、この関数の出力をなるべく訓練ラベル
に近づけたいというのがニューラルネットの学習になってきます。
このときの目的関数は、二乗誤差関数だったり交差エントロピーだったり様々ですが、ともなく何らかの目的関数が設定されたとしましょう。ニューラルネットでは目的関数を「損失関数」などと呼び、最適制御論では「評価関数」などと言いますが、まああまり気にしなくていいでしょう。
目的関数という言葉で統一していきます。
例えば二乗誤差関数の場合、出力が、単にラベルに近づくように
のような目的関数を設定します。目的関数の中身はニューラルネットの構造を代入すれば
などとなります。この時、文字に惑わされないでください。今、目的関数を最小化するために調整しようとしているのはの方です。
は単にニューラルネットへの入力であって、調整するものではありません。どんな入力が来ても、上手く出力を出してくれるような
を獲得したいのです。
従って、ニューラルネットワークの目的関数は通常
という形で表記されます。は「loss」の頭文字です。
ですから、ニューラルネットワークの学習とはを最小化することに他なりません。
そして、に対して何か条件を付けたい場合、例えば
がやたらめったら大きな値になってほしくない場合は
などの項を目的関数に追加します。
これは正則化とか、リッジ正則化などと呼ばれます。他にも
正則化などいろいろあります。いまは最小化問題なので、とにかく起こってほしくないことを項に追加していけば良いというだけの話です。
ニューラルネットの勾配降下法
パラメータを求める戦略
ともかく目的関数を決めたとしましょう。
そうした場合、をどのように求めましょうか。
まず戦略としては、適当なから開始して
の値を評価し、少しだけ変更した
で同じように
を評価し、さっきよりも下がっていれば変更後を採用すればいいということが考えられます。
イプシロンが適当な変更に相当する項です。
しかし、変更のパターンは無数にあり、どれくらい、どの成分を変更すればいいのかを決めるのは容易ではありません。従って、を適切に決められるようにしたいということが考えられます。
勾配降下法
その1つの方法が勾配降下法です。関数の微分は傾きを与えます。多次元においては関数のベクトルによる微分は、勾配ベクトルを与え、勾配ベクトルは関数の値を増やす方向を表しています。
そうであれば、勾配ベクトルと逆向きに進めば関数の値を減らす方向になるはずです。従って、の変更の仕方
を以下のように決めましょう
すなわち、
と値を変更すればいいということです。
は
に
を代入という意味です。(現時点での位置での勾配ベクトルがほしいから)
これをひたすら繰り返せばよく、更新の回数をとして一般的には
などと表現します。要するに勾配降下法とは文字通り、今の場所から勾配を下る方向に進んでいく更新方法です。
通常、代入の操作などは煩わしいので書かずに、教科書などでは
などと書かれているでしょう。は学習率で、勾配方向(の逆方向)にどれだけの大きさ進むのかを決めるスカラー値で、設計者が適当に決めます(大きければいいってもんじゃない)。
ニューラルネットの学習の基本とはコレだけです。
ただしはニューラルネット
の関数であり、
が
に対して非線形な形をしていて、微分は簡単には求まりません。この微分をエレガントに解く方法が誤差逆伝搬法と呼ばれる微分方法です。
ニューラルネットの損失関数
目的関数の凸性
誤差逆伝搬法によって、微分を求める方法も存在することですから、ニューラルネットの学習は簡単なように見えます。
しかし、忘れていけないのが凸関数かどうかです。ニューラルネットの目的関数は一般に
に対して非凸です。
勾配を下っていった先で、微分がになる点を見つけたところで、それが最小値かどうかは分かりません。むしろ局所的な最小解であることのほうが多いでしょう。
しかし、ニューラルネットの学習は、確かに最適化問題を解くことですが、我々がニューラルネットの学習をしたいのは、何か判別問題や回帰問題を解かせたいからです。
もしも最適化問題としては不十分で、最適化が済んでいなくとも、そのパラメータで十分に判別や回帰ができているのであれば問題ありません。ですから、通常、真の最適解かどうかは気にしません(というか確認の術がありません)。
最適化における課題
最適化における課題はむしろ、学習を如何に効率的に進めるかです。
最終的に最適解にたどり着くかは問題ではなくとも、なるべくはやく、そこそこの解にたどり着いて欲しいのです。通常、鞍点などを切り抜けるための上手い更新方法を考えるのがニューラルネットの最適化の主な課題です。
例えば、(鞍点ではありませんが)単純に以下のような関数の形をしていたとして、付近で勾配が異様に小さくなってしまうのが分かるでしょう。ここで学習は進むには進みますが、非常に遅くなってしまいます。

鞍点の場合は以下のような構造をしています。

これも赤い点の近くで学習が停滞してしまいます。
これを解決しようというのがAdaGradとかAdamとかです。
普通の勾配降下法の場合は
でしたが、右辺の第二項をあれこれ工夫してタダの微分じゃなくすという方法です。
あるいは目的関数自体がニューラルネットワークの構造に依存するわけですから、この構造を上手く問題に応じて工夫すれば、優れた目的関数の形になることが想定できます。
画像処理には畳み込み、音声・自然言語にはLSTMなどの構造を持たせることで、目的関数へのの現れ方が変わり、そしてデータの与えられ方も変化することとなります。