制御工学の基礎概念
制御工学とは
入力および出力を持つシステムにおいて、その(状態変数ないし)出力を自由に制御する方法全般にかかわる学問分野を指す。主にフィードバック制御を対象にした工学である。
(Wikipedia)
制御工学は、何らかのデータを入れたら、それに作用して何らかのデータを出力するシステムを適切に設計したいという目的で使われます。大抵の場合システムとは物理的実態を持っているケースが多く、例えばロボットアームというシステムに、電圧という入力を入れた際の、ロボットアームの手先の位置を制御したいという問題が考えられます。
ロボットアームの問題の例

上記のイラストのロボットアームの手先位置を制御することを考えれば、手先に速度をもたせる必要があります。そして、手先に速度を持たせるには、モータを回転させる必要があり、モータが回転するためには電圧が必要ということになります。
このように多重に変換を行うロボットアームにおいて、最終的に制御したい手先位置を、電圧をどのように変化させることで制御できるのかを考えるのが制御工学の一例です。
古典制御工学と現代制御工学
いまロボットアームの制御の例を見ました。
ここで手先の位置は出力であり、電圧が入力に相当します。
そして、モータの角速度のようなシステムの内部の値を状態変数と言います。
古典制御では主に入力と出力の値に着目しており、現代制御では加えて状態変数の値にも着目します。
古典制御は、多重に行われる変換の1つ1つを考えても全体を制御するには至らなかったことから(ワットの蒸気機関の例)、全体的な入出力関係をシステムとしてモデル化する必要があるということで生まれました。
一方で現代制御は、多重に変換を行うシステムの入出力関係のみでは制御ができない場合があることから、全体をモデル化したうえでその内部の情報まで用いようということで生まれました。
古典制御は割と手軽に、その割に強力な成果を得ることができ、現在でも広く使われています。現代制御はシステムの内部までモデル化を正確に行う必要があり、(モデルと現実の相違という点において)難易度が高く、広く普及するには至っていませんが、現代制御を使わなければならないものも存在し、一部使われています。
更に、現代制御の欠点を克服するポスト現代制御の研究もなされており、現代制御の正確さを損なわずに、かつモデルと現実の差異に対応できるような制御法(ロバスト制御)や、モデルが経年劣化など何らかの要因で変化していく場合に、それに順応して制御を変えていく方法(適応制御)などが考案されています。
PID制御
PID制御は古典制御の一手法
PID制御は古典制御の手法の1つであり、最も利用されている代表的な制御法です。これを知っているだけで多く実用的な制御の問題に立ち向かうことができると言っても過言ではないでしょう。
ロボットアームで言えば、手先の位置を制御したいという場合には、ある位置に手先を移動したいという目標値があるはずです。古典制御は入力と出力の値に着目した方法であり、出力を目標値に近づけるための入力値を求めたいというのが制御の問題になります。
その基本的な問題の解法は、「ある入力を与えた時の目標値と出力との偏差を見て、その偏差を小さくするように入力を修正する」というものです。その際の修正の仕方を適切に決める手法の1つがPID制御ということになります。

まず適当な入力を行ってみて、システムの出力をセンサで観測します。その出力の値と、実際に出力してほしい目標値との偏差を制御器に与えてあげると、制御器が良い入力を見つけてくれて修正してくれるというのが理想なわけです。
そのような具合の良い制御器の作り方の1つがPID制御ということになります。従って、図中緑の部分にPID制御器なるものが入ってくることになります。
フィードバック制御
上記のように現在の出力値を使って適切な入力を得る制御方法を、フィードバック制御と言います。
PID制御では出力フィードバックと目標値との偏差を取りますが、出力フィードバックの活用方法は他にもたくさんあります。例えば出力フィードバックに対して何らかの変換を施したあとに、目標値との偏差を取るなど、より複雑なフィードバックを使うケースもあります。
PID制御はフィードバック制御の一種と言え、目標値と出力との偏差に上手い変換を施してやることで修正した入力値を獲得することができます。
PID制御
PID制御の中身
制御の狙いと、フィードバック制御の概念を抑えたところで、PID制御の中身を見てみます。
(PID制御の概念図)
(Wikipedia:PID制御のブロック線図)
「Plant Process」は今回の話のシステムのことです。
入力を適切に決定し、システムの出力
をコントロールしたいという問題です。その際の目標値
であり、目標値と出力との偏差が
になります。
制御器の中身は、偏差を何やら「P」と「I」と「D」に渡して変換したものの和を取るという操作になってるようです。(ちなみに、Pだけを使う場合を「P制御」と言い、PとIを使う場合を「PI制御」などと言います)
PID制御の基礎概念
まず偏差については
であり、これは単純に目標値と出力値との差になっています。
仮に目標値がであり、出力値が
であったとすれば、偏差は
になります。偏差は目標値に対して出力がどれだけ足りていないのかを表しているわけです。
このように目標値と出力値の偏差が、であれば、何らかの修正を施して偏差を
に近づけたやりたいということになります。その近づける方法をあれこれ工夫したものがPID制御になります。
ところで偏差がであるときと、偏差が
であるときの入力の修正具合は同じでいいでしょうか?もしも修正を施して、偏差が
→
となった場合には、偏差を
に近づけるために同じ調子で修正を施した場合はどうなってしまうでしょうか。
考えつくのは、偏差が→
→
と振り切ってしまう(つまり出力値が目標値を通りすぎてしまう)ことです。本当にこんなに綺麗に(線形に)通り過ぎるかは定かではありませんが、これらを上手く調整してやる必要があるというわけです。
では「P」「I」「D」の効力についてそれぞれ把握していきましょう。
P制御
P制御の役割
P制御の役割は、出力と目標値との偏差に係数
を乗じるというものになっています。果たしてこれがどのように働くのでしょうか。偏差については
でした。
先ほど見たように、偏差が小さくなっていった場合は、それに応じて修正の量も変化させてあげる必要がありそうです。それを実現したのがP制御になります。
仮に目標値がであり、出力値が
であったとすれば、偏差は
になります。P制御では、入力の値を、偏差の大きさに比例して定めます。つまり現在の偏差が大きければP制御の影響は大きくなり、偏差が小さくなって目標値に近づくに連れてP制御は自身の役割を小さくしていくということです。
その際の係数がであり、P制御は単純に
という値を新たな入力値として考案してくれるというわけです。
非常に単純な仕組みではありますが、基本的に上手く働いてくれます。特に「線形システム」においては、入力の値と出力の値というのは線形に振る舞う(入力が大きくなれば、出力も同じように大きくなる)ので、この考え方は基本になってきます。
出力が目標値に対して足らないならば、入力を大きくする。
↓
出力が目標値にどれだけ足りていないのかを考慮して入力を大きくする。
という考え方をしているわけです。
P制御の欠点
P制御はPID制御の基本的な考えになってくれる一方で欠点もあります。
P制御が上手く働けば偏差は小さくなっていきますが、偏差がに近づいていくに連れてP制御の効力は失われ、実は完全に偏差を
にする前にP制御は役割を終えてしまうのです。
というP制御の式において、があまりにも小さすぎて、もはや入力も消失してしまうということです。すると、
は非常に小さいながらも残ってしまい、P制御の枠組みではこれを完全に消失させることができません。
ロボットアームが目標値に近づくに連れて動作が遅くなっていき、そして完全な目標値の一歩手前で止まってしまうということです。それでも良い場合もありますが、精密な動作が必要な場合は問題が生じます。
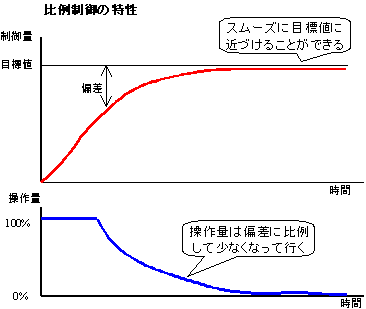
P制御(比例制御)の特性
このようにP制御で残ってしまう偏差を残留偏差と言います。
PI制御
I制御の役割
上記の問題を解決するためにPI制御というものが出現しました。PI制御を見る前にI制御について見ましょう。(通常I制御だけを使うことはありませんが、役割の確認をします)
がI制御の導く入力になります。これは今までの偏差の総和に比例した値を計算していることになります。残留偏差が残るのは、P制御だけの場合偏差に比例した入力を考えていたためです。偏差が限りなく小さくなってしまった場合、制御入力も小さくなってしまい、目標値に到達できないのでした。
一方I制御を導入すると、今までの偏差の総和を、すなわち過去の偏差の値も使って入力を決めるため、偏差がに近くとも制御入力がしっかり値を持つのです。
PI制御
通常はI制御はP制御の欠点を補うために使われます。
PI制御の特性
PI制御ではしっかりと目標値に到達することができます。
この場合の入力値の構成方法は
ということになります。
PID制御
D制御の役割
PI制御までで十分制御ができそうですが、まだ改善の余地があります。
ロボットアームが目標値に達するのは良いことだとして、その速さはどれほどのものでしょう。ゆっくりゆっくり目標値に近づくのと、素早く近づくのでは全く有用性が異なります。
D制御は目標値に達する速さを改善してくれる役割を持っているのです。
がD制御の導く入力値になります。偏差の時間的な変化に比例した値を考えるメリットは、外乱が生じた時などに顕著です。
PID制御
もしもPI制御で外乱が生じて、偏差が大きくなるようなことがあっても、P制御で調整はできるものの目標値に達するのに時間がかかってしまいます。I制御に至っては過去の偏差の和を考えているのであって、今瞬間的な外乱によって偏差に影響が起こったとしても、それを修正する能力はありません。
D制御は偏差の時間変化、すなわち瞬間的な変化に反応します。微分をするというのは傾きを求めることであり、傾きを求めることで、その周辺の値も近似することができるため、少し先の未来に偏差がどのような値になっているのかを見積もることができるのです。
偏差の具合の(少し先の)未来を考慮しながら入力値を調整することで素早く目標値に追従し、更に、外乱などの変化に強い制御を行うことができます。
PID制御の特性
PID制御では、D制御の挙動のお陰で、より積極的に制御量を調整することができます。
入力値は
で決定されるわけですが、が大きければ入力値は大きくなります。早く目標値に達したければこれらの係数を上げることが真っ先に思い浮かびますが、PI制御ではやたら制御量を大きくしてしまうと、目標値を通りすぎてしまうことが起こります。
もちろん、偏差が負の値になり、それに応じて入力を変化させるため、目標値に達することはできるのですが、余計目標値に達するまでに時間がかかってしまうので、そのようなことが起こらないように係数を決めるのが常套手段です。
しかしPID制御では、Dの役割によって偏差が大きくなった場合(すなわち目標値に近づいていった状態から、それを振りきって通り過ぎることが起こった場合)にも対応できるので、強気の制御が可能になります。
従って、PID制御では係数の設定を、PI制御よりも大きめに設定することのが普通です。
更に制御を詳しく学ぶには
周波数解析
入力や出力がどのような波形であろうと、フーリエ変換の枠組みを使えば三角関数の和で近似することが可能です。三角関数の和で表現できたならば、出力の値を操作する際に考えるべきは、制御の仕方によって、いろいろ周波数な三角関数の振る舞いがどのように変わるかということになります。
制御工学では通常、ラプラス変換が用いられ、入力と出力、そしてシステムを周波数領域で考えるのが常套手段となっています。周波数領域で考えると、出力の振る舞いを三角関数で議論ができ、どのような周波数が増幅され、どのような周波数の位相に遅れが生じるのか詳細を検討することができます。
例えばI制御というのは積分であり、これは三角関数で見た時、必ず位相の遅れを生じさせてしまうということや、D制御は逆に位相を進ませることができるということが分かります。
現代制御
現制御には応答性だけでなく、安定性など議論すべき課題は他にもあり、古典制御では安定性に関する議論は不十分でした。現代制御は、システムの内部状態にまで目を向け、出力のフィードバックのみならず、状態変数のフィードバックも使って正確な制御を達成します。
現代制御では状態空間モデルが用いられ、周波数解析とはまた違った視点から解析が行われます。数学的な難易度で1つの山場ですが、得られるものもたくさんあるでしょう。
ポスト現代制御では、代表的なものにロバスト制御(特に制御)や適応制御があります。適応制御の方は、機械学習とも関連が(比較的)深い分野で、ニューラルネットなどが応用されるケースもあります。強化学習などとの関連も深く、私も是非更に学びたい分野です。