
学習の種類
教師あり学習
教師あり学習では、入力データとそれに対する解答をセットでシステムに与えます。
システムにデータを入力すると、何らかの出力を行います。もしもその出力が解答と違っていれば、システムの出力の仕方を僅かに変更するという形で学習を進めていきます。
システムの出力を
データを
解答を
システムの出力と解答との違いの尺度を
としておき、いろいろなに対して、その解答
とシステムの出力
が近づくように
を調整することになります。
データと解答の組をたくさん準備しておき、十分に学習を行いを調整すれば、未知の問題にも答えられるようなシステムが完成することが期待できます。
教師なし学習
教師なし学習は、データに対する明確な解答がわからない場合に用いられます。
システムはデータが入力されると何らかの方法によりそれを変形しますが、どのような変形をして欲しいのかは人間側が与えることになります。
例えば、とN個の問題がある場合、近いデータ同士をまとめてほしいとか、データの次元が高い場合に、情報を保持しつつ、より低次元なデータに変換してほしいなどの要望が考えられます。
半教師あり学習
半教師あり学習は、データとそれに対する明確な解答が分かるものと分からないものが入り乱れている場合に用います(正確なデータが集めづらい場合や、解答をデータに付与する作業が困難である場合)。
強化学習
ハッキリとした答えがわからない
強化学習は明確な答えが分からない場合に用いられます。
しかし教師なし学習というわけではありません。答えはわからないが、良さそうか悪そうかということの提示は行うのです。つまり「良いか悪いかだけなら言及できそうだが、正確な解答を提示することができない」ようなケースを扱うことになります。
良さそうか悪そうかの判断方法自体もわからない
ここで、もしも仮にハッキリ答えを知っているのであれば、その答えからどれだけ離れているのかを測ることによって、良さそうか悪そうかを提示することができます。しかし実際にはハッキリとした答えがわからないケースを扱っているのでこれはできません。
強化学習では、良さそうか悪そうかを判断するための基準自体も、学習の過程で決めていくことになります。
教師あり学習では、例えば最小二乗誤差であったり交差エントロピーであったりが損失関数として用いられます。この損失関数を小さくすることが学習となるわけですが、強化学習では何を小さくすれば良いのか(あるいは大きくすれば良いのか)すらも分からないのです。
問題設定は遥かに複雑
更に、強化学習は、システムの出力に応じて周りの環境が変化していくような場合も想定します。通常の機械学習では、問題と解答は常に静的に定められており、「これが入れば、これが解答」と決まっているのですが、強化学習では、「これが入っても、状況に応じて対応を変える」ことを学習させることになります。
囲碁で、相手が「A」という位置に石をおいた場合、これを入力としてシステムがどこに石を置き換えすのかを「教師あり学習」させることができるでしょうか。
相手が「A」におけば自分は「B」に置くと良いとはっきり言えるでしょうか。言えないはずです。それは状況に応じて変えなければなりません。そして、自分自身の対応次第で、相手の対応も変わり、盤面という環境が刻一刻と変化していくので、更に次に自分がどのような行動を取るべきかを知るのは非常に難しい問題です。
スポンサーリンク
強化学習を理解する特殊例

強化学習の難しさと課題点
強化学習は多くの機械学習と比べて、学習の仕方や問題設定が異なっていることを説明しました。その最たるものは以下の2つです。
・教師あり学習に比べ、答えを直接提示できない
・強化学習では評価関数自体も学習の過程で推定しなければならない
強化学習がなぜこのような難しい問題に取り組む必要があったのかを見るために(つまり強化学習の狙いを知るために)、「n本腕バンディット問題」というものを見てみましょう。
n本腕バンディット問題
問題の状況
問題状況は至ってシンプルです。
スロットがn台あります。それぞれのスロットは当たりを出す確率が異なっており、私はたくさん当たりを出したいので、プレイする中でスロットの当たる確率を見積もりながら、より当たりの回数を増やすためのスロット選びをしたいという状況です。(もっと問題を複雑にすれば、当たった際に得られる賞金の額が違ってもいいです。確率が低くとも、賞金額(報酬)が高いものを選びたい場合もあるからです)
このような問題状況において、n台のスロットを1台のスロットにn本の腕(選択肢)があると見るため、「n本腕バンディット問題」と呼ばれます。

n本腕バンディット問題の形で問題を言い直します。
n本の腕から1本選ぶことをプレイと呼びましょう。そして実際にスロットを回すことを行動と呼びましょう。プレイを繰り返す中でそれぞれの腕の当たる確率を見積もりながら、限られた回数でたくさんの当たりを出す(たくさんの報酬を得る)方法を考えたいということです。
ここで私達は適切な行動を取る方法を考えなければなりませんが、そのためには、プレイ(腕の選び方)を工夫するよりほかありません。
行動の価値
どのようなプレイをするかは、恐らく過去の経験から考えるしかないでしょう。プレイし、行動し、その行動の結果を観測しながらプレイの仕方を模索していくのです。プレイの仕方を模索するために、行動の価値という概念を考えましょう。
行動の価値は、「行動に対して得られる報酬の期待値」として定義します。ここで言えば、スロットの腕を1つ選択した際に得られる賞金の期待値ということになります。従って行動1つ1つに対して価値が定義され、それぞれ異なった価値を持っていることとなります。
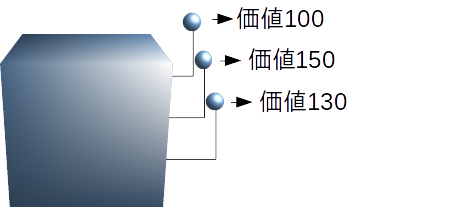
そうともあれば、仮に行動の価値が全て既知であるならば、この手の問題を解決するのは簡単です。もっとも価値が高い行動を選択し続ければ良いだけです。
しかし、行動の価値はプレイをする中で見積もっていかなければなりません。今見積もられている行動の価値というのは、あくまで今までのプレイの結果であって、本当の価値は違っているかもしれないです。
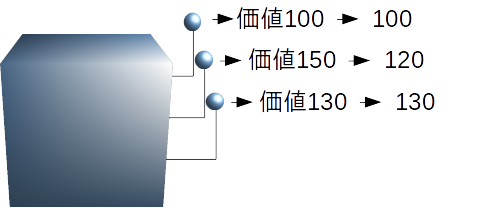
しかし、行動を移すうちに価値の推定値が変化していったとしても、そのときそのときの行動の価値が見積もられているのですから、結局はそのときの価値の最大値を見つけることは可能です。
上記の例で言えば価値150のレバーを選択しているうちに、どうも当たりが弱いと感じるようになり、価値が120に更新されたのであれば、次からは価値130のレバーを選択するということができます。
しかし、そう考えると果たして価値130のレバーを選択するのは懸命な判断でしょうか。もしかしたら価値100のレバーを調べ上げていくうちに、もっと高い価値を有することが判明するかもしれません。
要するに、現在までに得られている価値の知識が不完全だとすれば、本当の価値の知識を獲得するために、あえて探査してみるということもできるはずです。
知識利用と探査
現在の価値に従って、そのときそのとき最大のものを選ぶ方法を貪欲法(グリーディ法)と言います。貪欲法は純粋に今もっている知識を利用するということになります。一方で貪欲法を用いないということは、あえて他の選択肢の本当の価値を探査することを意味します。
もちろん、本当の価値を有限のプレイ回数で知ることは難しいので、時によって探査か知識の利用かを選択しなければなりません。また、残りプレイ回数が1回しか無いのであれば、当然貪欲法を選択するほかないわけで、状況によって取る選択は異なってきます。
すなわち知識利用と探査を上手く使い分けるのかも課題になっているというわけです。
行動価値関数と行動の決定
Q関数
これまでの話の通り、行動の評価をしてやるために、行動に対する価値関数の推定値
というものを考える必要があります。しかも、価値の推定値というのはどうもプレイをしていくうち変化していくわけですから、プレイ回数を
回とすれば、
行動価値関数の推定:
なるものを求めていく必要があるようです。通常Q関数と呼ばれます。
また、(それを知る由も無いのだが)真のQ関数というものも存在するはずであり、それをと書くことが多いです。
貪欲法による行動の選択
貪欲法では、を最大とするような行動
を選択するので
を選ぶこととなります。このような選択をする限り、行動価値関数の推定を進めていくことは困難になります。
従って、時折上記以外の選択を混ぜていく方法が考えられます。
混ぜ方は最も単純な方法で、小さな定数の確率で貪欲法以外の選択をするε-貪欲法があります。もしも、プレイ回数を無限回に増やせるのであれば、探査が十分に行われ、真の
が得られることになりますが、実用上の有用性を提示することはできません。
ソフトマックス行動選択
ε-貪欲法では、小さい確率で貪欲法で選ばれる選択肢以外の行動を均等な確率で取ることになりますが、果たしてこれは有効な方法でしょうか。もしかしたら現時点で価値が異常に小さい行動が分かっていれば、その行動に関して探査をする必要はないかもしれません。なんといっても実問題ではプレイ回数は有限なのですから。
その場合は、現在の価値に合わせた重み付けをする方法があります。
例えば行動が3種類あるならば、と、現在の価値の見積もりがあるはずです。その場合に行動
を選択する確率を
とするのがソフトマックス行動選択です。現在価値が最大の行動が選ばれやすいのですが、(価値の大きさを反映した)小さな確率によって異なる行動を選択します。
一般に行動を選択する確率を
と記述することになります。
他にも様々な方法がありますが、これらの手法を用いて、知識利用と探査のバランスを取り、価値関数を見積もりながらも学習を進めていくこととなります。
最後に
さて、行動価値関数がある中で、どのように探査と知識利用を選択するのかが重要であることを述べてきました。しかし、まだ如何にして行動価値関数を推定するかについて述べていません。
ある行動を選択した場合に行動価値関数が変化していく様をどのように記述するかが問題です。それらを記述したものが強化学習となります。
DQNで有名な深層強化学習は、行動価値関数(Q関数)を深いニューラルネットによって表現し、推定していくことが肝となっております。やはり行動価値関数をどのように記述し、推定していくかが強化学習では重要なことだと伺えますから、まだまだ抑えなければいけないポイントはたくさんあるでしょう。
しかし、今回の記事によって、通常の機械学習と強化学習では問題設定が異なること、そしてどのようなケースが想定されているのかも理解できたかと思います。余力があれば、引き続き強化学習について詳しい記事を書いていきたいと思いますのでよろしくお願いしたします。
行動価値関数に関する続編記事
行動価値関数をどうやって作るのかの基本を解説しています。
強化学習を学ぶための書籍
これからの強化学習は比較的最新の知見も含まれている強化学習の本です。強化学習をある程度知っている人が読むべき本になります。
強化学習を初めて学ぶ人は古典的名著である強化学習をおすすめします。平易な文章と、シミュレーションを載せており、数学的な基礎があれば十分に学んでいくことができるでしょう。

- 作者: 牧野貴樹,澁谷長史,白川真一,浅田稔,麻生英樹,荒井幸代,飯間等,伊藤真,大倉和博,黒江康明,杉本徳和,坪井祐太,銅谷賢治,前田新一,松井藤五郎,南泰浩,宮崎和光,目黒豊美,森村哲郎,森本淳,保田俊行,吉本潤一郎
- 出版社/メーカー: 森北出版
- 発売日: 2016/10/27
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る

- 作者: Richard S.Sutton,Andrew G.Barto,三上貞芳,皆川雅章
- 出版社/メーカー: 森北出版
- 発売日: 2000/12/01
- メディア: 単行本(ソフトカバー)
- 購入: 5人 クリック: 76回
- この商品を含むブログ (29件) を見る
2016年NIPSでも強化学習は話題だった
NIPSでもバンディット問題は取り上げられており、強化学習自体の話題も豊富でした。