
はじめに
ニューラルネットワークを始める際には色々学ばなければならないことはあると思いますが、今回は線形変換と、特にその後に用いられる活性化関数に期待されていることをまとめておきたいと思います。
線形変換(Linear)
数式
に対して出力
は
となります。正確には線形変換とはのことで
は含みませんが、ニューラルネットでは通常上記の演算を線形変換(Linear)と言います。Σを使って表記すると
と表されます。
効果
である場合は、
次元のベクトルを
次元に変換し、ベクトルの回転と拡大・縮小を行います。
次元を変更することは以下の2つの効果が期待できます。
次元を下げる場合
元々のベクトルに格納されている成分が冗長な情報を有している、あるいはノイズを含んでいる場合に、それらを取り除く効果が期待できます。
教師なし学習である主成分分析・独立成分分析や、教師あり学習である線形判別分析も本質的には線形変換のみで達成されるものであり、実はこの変換だけでも十分な能力を持っていると言えます。
ただし、多くの線形変換を用いる手法は、損失関数がひと工夫されており、目的に応じた良い線形変換が見つかるように考慮されています。
次元を挙げる場合
元々のベクトル(データ点)の表現では線形分離ができないが、高次元に埋め込むことで分離できる表現を見つける効果が期待できます。
ニューラルネットでは活性化関数(非線形関数)を使って、線形変換されたデータにさらなる変換を施すのがセットになっています。非線形変換が加わると、線形変換だけでは表現できなかったことも表現できることが期待できます(曲線を考えられる。あるいはデータ空間を曲げられる)。
サポートベクターマシンのカーネル法(特にガウスカーネル)は、事実上無限次元の空間へデータを移すことで、非常に高い精度で分離可能な境界を見つけます。
活性化層
数式
活性化層は、通常「層」という扱いはしませんが、近年のディープラーニングのフレームワークでは、個別に層として考慮したほうが分かりやすい場合が多いです。
に対して活性化層の出力
は、非線形関数
を用いて
この非線形関数はベクトルの各要素ごとに演算を行います。例えばという非線形変換であった場合に、
というデータが入れば、
と言った具合になります。実際に使われる活性化関数には以下のものがあります。
活性化関数の種類
シグモイド関数

ステップ関数を微分可能にしたもの。
双曲線正接関数

双曲線正接関数はシグモイド関数の線形変換であり、正にも負にも値を取り、原点を通ることから後に採用されるようになった。
ランプ関数(ReLU)
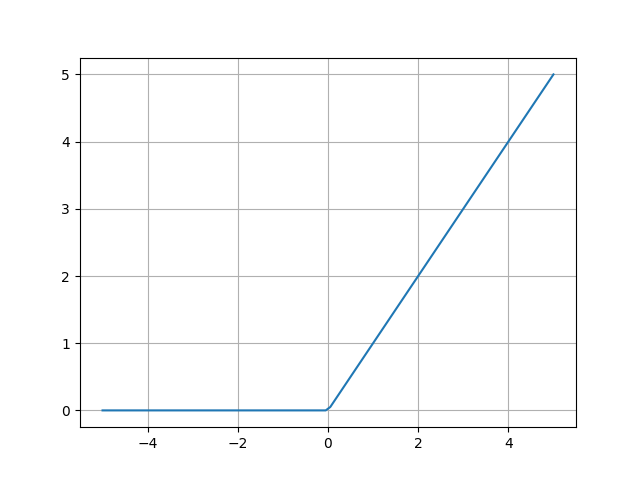
シグモイド関数や双曲線正接関数は、原点から遠ざかる(値の絶対値が大きい)ほど、勾配が無くなるため、一度ユニットが大きな値を持ってしまったら学習が停滞する問題があった。ランプ関数では勾配消失問題が経験的に解消されることが知られている。
切断冪関数

ランプ関数は、が負であれば
を返し、
が正であれば
を返す。切断冪関数では、
が正であれば
を返す点が異なる(
がランプ関数)。(画像は
の場合)
動径基底関数

動径基底関数はカーネル法やウェーブレット変換などでも用いられる関数である。(画像は)の場合。
ウェーブレット
はある条件を満たす関数。
と
で平行移動と拡大縮小をそれぞれ担っている。
として動径基底関数を選べば、
となる。(の調整は
に吸収されている)
と
を調整することで、時間周波数解析が可能。ニューラルネットワークに応用する場合は1次元の時系列データ
を
とベクトルに格納することで、時系列解析が可能であると提案されている。
上からの例。ただし
。(
に値をもたせればその分平行移動する)



ReLUに関して
シグモイド関数は微分可能にするという数学的な発想で生まれました。微分可能にしたことで、誤差逆伝搬法という画期的な学習手法が使えるようになりました。その後、双曲線正接関数なども登場してきます。
現在はランプ関数(ReLU)が最も使われているのでこの関数を中心に説明します。
勾配消失の緩和
まず以下のReLUの出力を見ましょう。

誤差逆伝搬法では出力値の微分が学習の係数に入ってきます。ReLUは入力値が正であれば、入力値をそのまま出力します。このとき微分は必ず1の値を取り、出力の値が学習を邪魔することが一切無くなります。
これがシグモイド関数(以下)の場合だとどうでしょうか。

入力が大きくなればなるほど、微分の値は小さくなっていきます。入力の値が仮に偶然10などになった場合、微分の値が極めて小さな値を取ることが想定できます。この小さな値が学習の係数に掛かってきてしまうため、(本来はまだ最適解にたどり着いていないのに)学習が滞ってしまう勾配消失問題の引き金になってしまうのです。
(実際には0になるわけではないのだが、多層の場合に、複数の層でこのようなことが起こると、誤差逆伝搬で誤差を伝えていくうちに、非常に小さい数の掛け算が行われていった挙句、誤差が正しく伝搬されなくなる)
ネットワークのスパース化
ReLUのもう1つの特徴としては、ネットワークのスパース化に貢献するという点です。ニューラルネットワークがスパースであるとは、出力が0であるユニットがたくさんある状態を指します。
仮にあるユニットへの入力が0未満になると、出力が0になります。そしてその領域において、ReLUの微分は0であるため、これが学習の係数に掛かるため、結果としてそのユニットは全く学習が行われなくなります。

そして、学習が行われなくなったユニットに対するパラメータは変化しないため、入力も変化せず(0未満のまま)、出力がその後ずっと0となります。学習は残ったユニットだけで行われるようになりますが、ニューラルネットワークは元来冗長であるため、返ってユニットを厳選していくこととなり、良い成果が得られるのだと言われています(事実上学習するパラメータを厳選していることになる)。
ReLUの派生
ReLUの活躍を見て、この活性関数を改造していく試みが多く存在します。
ReLUの派生はいろいろあるんですけども、とりあえずやってみた感満載です(別に良いんですけど)。他のタスクに使えるのか(効果の再現性的なもの)は謎です。だいたい何がどう嬉しいのかよくわからないものが多いです(勉強不足なだけかもしれません)。
シグモイド関数や双曲線正接関数について
シグモイド関数と双曲線正接関数に関しては、その値域に着目して利用がなされています。
例えばHighway Networkでは、シグモイド関数が0〜1の値を取ることに注目して、「値をそのまま通過」と「値を変換する」の混合割合を調整するゲートとして用いています。
このゲートという発想はLSTMで用いられているもので、LSTMでは記憶保持や、過去の値をどれくらい使うか、現在の値をどれくらい通過させるかなどに使われています。
最後に
現状、タスク毎に活性化関数を変えたほうがいいという状況です(ReLUの派生が良い成果だすこともある点を考慮すれば)。
ところで、ニューラルネットワークのパラメータは基本的に膨大で、明らかに分類タスクや回帰のタスクにおいて冗長な形式となっています。そのような観点からスパース化は重要な技術だと考えられており、ReLUはスパース化が達成でき、かつ計算も速くなるので迷ったらとりあえずこれを使っておけばいいでしょう。
変換が単純であるが故に表現力は単体では乏しいですが、ニューラルネットを多層にすればそんなの問題無し(どころか何度も言うが冗長)、むしろバランスが取れると言ったところでしょう。