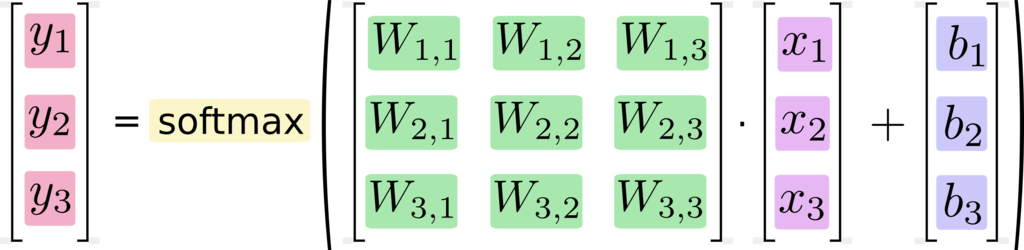事前知識
ニューラルネットワークの構造
ニューラルネットワークでは入力されたデータを分類するために、入力層には入力データの要素数と同じ数のユニットを配置し、出力層には分類すべきクラスの数だけユニットを配置します。
中間層の数や、中間層のそれぞれのユニットの数は勝手に決めていいです。
入力データがn次元、クラスがD個あるならば、入力層のユニットはn個、出力層のユニットはD個ということです。
出力層は何を出力するのか
出力層は、データがあるクラスに属する確率を出力します。
クラスが3つあれば出力層のユニットも3つで、出力されるベクトルは3次元になります。入力データに対する出力が以下であったとしましょう。
すると、クラス1に属する確率が0.11、クラス2に属する確率が0.82、クラス3に属する確率が0.07と解釈することができます。この場合は、クラス2に属する確率が一番高いので、データはクラス2であると判定することになります。
ニューラルネットワークの学習
ニューラルネットワークを学習するというのは、すでにクラスが分かっているデータを大量に集め、それをニューラルネットワークに与えることで、与えたデータを上手く分類できるようにネットワークの重みを調整していくことです。
具体的には、データとその正解ラベル
をセットで渡していきます。
データがクラス3に属するならば、
の3番目の要素のみを1に設定し、他を0にしておきます。
当然、与えられたデータを上手く分類するように学習するだけですから、新しいデータに対して上手く行くという保証はありません。新しいデータに対しても分類が上手く行くためには、そもそも手持ちのデータの質が良く、更にネットワークはデータの個々の特徴ではなく本質的な特徴を捉えなければなりません。
それが可能なように学習を工夫する必要があります。通常、学習をさせすぎると、手持ちのデータにだけ帳尻を合わせたニューラルネットワークが完成してしまいます。これを過学習と言います。基本的に一旦手持ちのデータを上手く分類できるようにしてから、過学習を緩和するように学習の仕方を調整していくことになります。
出力層の活性化関数にはソフトマックス関数が使われ、学習の損失関数には交差エントロピーが用いられます。これによって、出力が確率であることが保証されます(以下を参考に)。
仮に分類問題を解きたいのにも関わらず、出力層を全然関係ない活性化関数にしたり、全く異なる損失関数にしてしまった場合には、なんだか関係ない何かが学習され出力されることになってしまうので注意してください。
ミニバッチ学習
通常の学習では、入力データと正解ラベル
のセットをすべて一気に与えます。つまり、
とすべてのデータに関して学習を繰り返すことになります。この方法はバッチ学習法と言います。
すべてのデータを考慮したニューラルネットワークの更新を行うため、最も妥当に感じる方法です。
一方で、とりあえずだけ与えて、次には違うデータ[\bf tex:x_m]を与えるという具合に、1回1回の更新はただ1つのデータのみを考慮して行う方法を確率的勾配法と言います。すべてのデータを与え終わって、初めて1回学習したことになります。
これは1つのデータしか考慮せずに更新を行うため、他のデータにとっては悪いニューラルネットに変化してしまう場合もあります。一方で、そのような不規則な学習が結果的に良い方向につながる場合もあります。
バッチ学習ではすべてのデータを同時に考慮するため、全データに取って良い方向に必ず学習が進みます。一方で、確率的勾配学習ではデータを与える順序によって、更新の仕方が異なってき、不規則性が生まれます。学習が全データにとって、良い方向にも悪い方向にも進みうるのです。このことによって、ときとして鞍点(学習が停滞するところ)を早く抜け出したりすることに役立ちます。
この両者の良い所どりをしようとしたのがミニバッチ学習法です。
データをとすべて与えるのではなく
と3つずつ与えようという具合です。この場合ミニバッチサイズが3であると表現します。
このミニバッチサイズを調整することで、確率的勾配学習とバッチ学習の間を調整することができるのです。
まとめ
まとめは簡潔に数式を用いて書きます。
ニューラルネットワークはデータ
を与えたら出力
を返します。学習では、この出力
がデータ
の答えである
に近づくように学習します。
としてがなるべく
に近づくように
を調整するということです。
と
の近さは交差エントロピーで測ります。交差エントロピーが小さいほど近いということになります。この交差エントロピーを損失関数として、損失関数を小さくするように
を探していくのが学習です。間違っても分類問題で二乗距離などを近さの指標にしないこと。損失関数にはちゃんと意味があります。
また学習時にはミニバッチ学習を行うのが一般的で、ミニバッチサイズを上手く調整することで確率的勾配学習とミニバッチ学習の間を調整することができます。
MNIST For Begginers
はじめに
TensorFlowのチュートリアルには「For Begginers」と「For Experts」があります。
前者の方が基礎から解説を行っており、後者はある程度知識を前提として話を進めています。
前者では通常のニューラルネットワークを用いており、後者ではそれに加え畳み込みニューラルネットワークも扱っています。
基本的にBigginersが分かれば、TensorFlowで簡単なネットワークを扱うことはできるはずです。畳み込みニューラルネットワークもTensorFlowではさほど難しくありませんが、各パラメータが何を意味しているのかを知るには、畳み込みニューラルネット自体を勉強しなければなりませんので、今回は予備知識が少なくて済むBigginersを解説します。
MNISTとは
MNISTは手書き文字の画像データセットで、新しい手法を試す際によく使われるデータセットです。MNISTは基本的にかなり高精度が出せる簡単な問題であるので、ここで新手法の出来栄えを測ることがよく行われます。
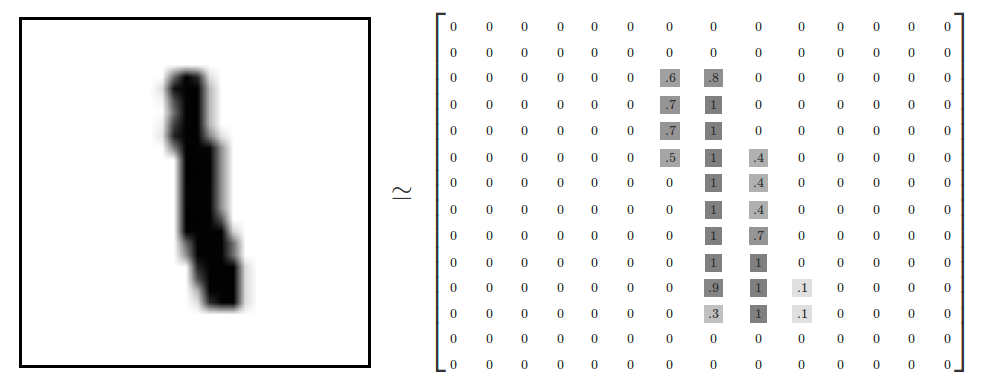
手書き文字の画像は以下のようなものです(TensorFlowより転載)。
人間ならば、ある程度字が崩れていて、異なった人が書いた文字でもちゃんと識別できるでしょう。ニューラルネットワークにも少しくらい字が崩れていてもちゃんと識別できるようにさせてあげようという問題です。数字は「0〜9」の10通りありますので、10クラスに分類するニューラルネットワークを構成していきます。
この画像は28×28のピクセル画像で、黒い部分に何らかの値を持っており、白は0の値になっています。値が大きいほど濃い黒色をしています。
ニューラルネットワークは、この数字のパターンを学習して識別をするという仕組みです。
Bigginersで使うニューラルネット
問題設定は、28×28のピクセルデータを入力して、10クラスの分類問題を解くというものです。
ここで今回使うニューラルネットワークは普通のニューラルネットワークですので、のユニットを入力層に配備します。データをすべて一直線上に並べてしまうということです。こうしたとしても、描かれている数字に応じて、784次元のベクトルが取る値は違ってくるはずなのできっと分類できるでしょう。
よって、入力層は784個のユニットを準備し、出力層は10個のユニットを準備します。
ニューラルネットワークは、784次元ベクトル
を10次元ベクトル
に変換するような構造を持っていることになります。
Biggnersでは、最も単純に入力層と出力層だけのニューラルネットワークを使います。
従って深層学習ではありません。
しかしこれがすべての基礎になります。結局、すべてのニューラルネットが最終的には出力層でソフトマックス関数によって出力を行うためです。今回は構造が単純なだけで本質的な部分は深層学習でも同じです。
ニューラルネットワークの数式
今回は入力層と出力層しかありません。
というニューラルネットワークを具体的に書き下しましょう。
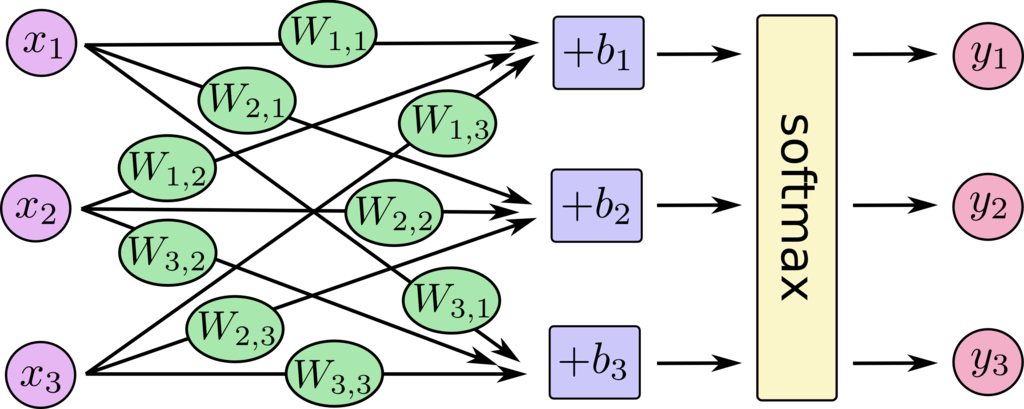
まずネットワークの構造は以下の図で表されます(便宜的に入力の数が3、出力も3になっていますが、今回の問題は本当は入力784で出力が10です。)。
の
番目の成分を
とし、同様に
を考えると数式では
となります。に重み
を掛けて、バイアス
を加えたものを、ソフトマックス関数で変換して出力します。
行列表現にすると以下のようになります。
これは行列の操作に慣れている人ならすぐに分かることでしょう。本ブログでもΣ表現と行列表現を自由に行き来できることの重要性は強調しています。
チュートリアルになぞらえるとこの表現の変換は、以下の図で説明できます。
について成分ごとに並べた際の式。
これをバイアス項をとして分離することで
を表したもの。
当然今回の問題ではは784次元で
は10次元です。
は
の行列になります。
今回はこのようにして得られるを正解ラベル
に、
と
を調整して近づけていきます。
Tutorialのコードの解説
全コード
とりあえずチュートリアルで使われているコードを通しで記載します。
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)import tensorflow as tf
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))y = tf.nn.softmax(tf.matmul(x, W) + b)y_ = tf.placeholder(tf.float32, [None, 10])cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)init = tf.global_variables_initializer()sess = tf.Session()
sess.run(init)for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))データのインポート
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)この部分で、MNISTのデータをインポートしています。
TensorFlowのインポート
import tensorflow as tfこれでTensorFlowが使えるようになります。
入力データの次元をセット
x = tf.placeholder(tf.float32, [None, 784])ここでは入力データの次元をセットしています。
入力データは784次元なのでそのようにセットされています。
Noneの方は、入力データをどれだけ与えるのかをまだ決めていませんということを示しています。これによって入力データの数が任意であると設定されます。
実際、ミニバッチ学習ではミニバッチサイズを色々変えてみたいという場合があるので、一度に与える学習データのサイズは任意にしておいたほうがいいでしょう。
ニューラルネットのパラメータをセット
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
今回使うニューラルネットは
ですから、行列とベクトル
を1個ずつ準備しておけばいいですね。
入力の次元がで出力の次元が
なので、
には上記の値をセットします。
ただし注意が必要なのは、上記の数式ではは「
」次元の行列ですから、ついコードでもこの順番で書きたくなるかもしれませんが、tensorflowの実装では逆になっています。
次元から
次元にするような行列ということで覚えればいいでしょう。
実装の中身がどうなっているかは調べていませんが、
という数式の転置を取ると
と表すことができ、このような場合にはは当然
次元になっています。
経験上、機械学習では数式が転置された状態で実装されていることが多いように思います。つまり、データは横ベクトルで、データを下方向に並べているということです(まあどっちでもいいですけど)。
ベクトルは10次元なのでそのようにセットされています。
出力の設定
y = tf.nn.softmax(tf.matmul(x, W) + b)これによって、出力が計算されています。これは
を書いているに過ぎません。これを見るとやはり転置で
と実装されているのでしょうかね(どっちでもいいですけど)。
正解ラベルの次元をセット
y_ = tf.placeholder(tf.float32, [None, 10])これで正解ラベルのセットをしています。正解ラベルは次元でしたね。
Noneの方はデータをどれだけ与えるかが任意であるということです。
このコードでは正解ラベルは「y_」ですが、今まで数式で説明してきたのことです。コードの出力「y」と被るので、自分で書くときは他の記号にしたほうがいいでしょう。
損失関数の定義
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))このコードで損失関数を定義しています。
-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])の部分が交差エントロピーです。これをちゃんと問題に応じて設定しないと変なことになります。
回帰問題ではここが二乗誤差になっていますが、そのコードをコピーして分類問題に使ってみれば変な結果になることが分かるでしょう。
学習方法を決定
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)0.5が学習率です。大きければ大きいほど、更新を大きく行います。たいてい大きくし過ぎるとどんどん精度が悪くなっていくのが見られるでしょう。あるいはヤケに良くなったり悪くなったりが激しいという具合です。
小さすぎると学習が非常に遅くなります。本当に少しずつしか進んでいきません。ここは適宜調節するしかありません。この更新は、先ほど定義した損失関数を減少させるように行われるよう設定されます。
.minimize(cross_entropy)の部分が最小化すべき値を設定しているところです。
更に
tf.train.GradientDescentOptimizerの部分は学習の最適化法を指定しています。これは最も基本的な方法ですが、他にもAdamやAdaDeltaなども実装されています。上記の部分を
tf.train.AdamOptimizerなどと設定すれば使うことができます。
初期化
init = tf.global_variables_initializer()TensorFlowではニューラルネットの学習を始める前にこの操作が必要です(じゃないと動かないそうです)。
初期化の実行
sess = tf.Session()
sess.run(init)sess.run()で実際に実行を行います。これで準備を整えることができました。
学習を実行
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})学習を1000回繰り返します。そしてミニバッチサイズは100です。
精度の確認
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))このコードにより、ニューラルネットの出力ベクトルで最も大きかった成分の番号(つまり判定されたクラス)と、正解ラベルで最も大きな成分の番号(正解クラス)が等しいか否かを調べます。
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))によって、出力と正解を調べた結果を獲得します。
例えば[True,True,False,True]ならば[1,1,0,1]となり、平均が3/4で0.75と正解率が出ます。
最後にテストデータでニューラルネットを評価
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))これによって、学習に用いていないテストデータをニューラルネットに入れて、上記のように正解ラベルとニューラルネットの予測を比較し、正解率を表示します。
おそらくこのモデルならば92%くらいの正解率です。
しかし、MNISTでこれは非常に低い値です。
今回使ったのが簡単なモデルだったからです。もう少し複雑なものを使えば99%をこえることも簡単でしょう。
まとめ
今回のコードは
データをインポート
入力データの次元を決める
ニューラルネットの構造を決める(=パラメータを準備する)
出力を決める
正解データの次元を決める
正解データと損失を使って損失関数を定義する
学習方法を決める
学習する
評価する
という手順です。この流れをひと通り体験したら、あとはニューラルネットの構造を変えてみるとか、学習の方法を変えてみるとかは簡単にできるでしょう。
ニューラルネットの構造を工夫するにはニューラルネット自体に詳しくならなければなりません。
どういう構造ならば上手く識別ができるようなモデルになるのかなどを考察するのは簡単ではありません。画像認識の場合は畳み込みニューラルネットが非常に有用であることが知られています。
勉強のために
なども参考にしてみてください。