バイアス-バリアンス分解：機械学習の性能評価

f:id:s0sem0y:20170505211841j:plain

はじめに
- この記事で理解できること
- バイアス-バリアンス分解とは
予測性能
損失関数の期待値とその分解
バイアス-バリアンス分解
全体のまとめ
- 参考となる書籍

はじめに

この記事で理解できること

・学習によってモデルをフィッティングさせる概念を理解できる。

・機械学習で回帰問題を解決する際に、未学習や過学習を評価できる。

・特に $L1$ , $L2$ 正則化などが及ぼす影響を理解できる。

バイアス-バリアンス分解とは

実データを用いてモデルをフィッティングした場合には、真のモデルとの間に「バイアス、バリアンス、ノイズ」の3つの要素によってズレが生じます。このズレ具合を評価することで（特にバイアスとバリアンスを比べることで）未学習や過学習などを直感的に理解できるようになります。

予測性能

未学習とは

まず機械学習における未学習とは何かを説明します。

読んで字のごとく、学習が不十分なために、データを表現するモデルが全く得られていないような状態です。通常、訓練誤差が十分に減少していなければ未学習だと言えます。

これを解決するのはそれほど難しくなく、ハイパーパラメータを調整しながら、とにかく訓練誤差が下がるまで実験を繰り返せばいいです。基本的に、この訓練誤差をある程度下げられるようになってから、後の細かい調整を行っていきます。

過学習とは

学習済のモデルが過学習になっている場合は、未知の新たなるデータを入力した際の予測性能が著しく低いです。つまり訓練誤差を下げることに集中しすぎてしまい、与えた訓練データを「無理やり」表現するようなモデルになってしまった状態です。

機械学習の本来の目的は、未知のデータを予測することであり、その予測を行うために手元にあるデータからそれが可能なモデルを構築するのを「学習」と言いました。過学習は典型的な学習の失敗例です。

未学習だけの場合は解決は簡単ですが、これを克服しようと訓練データを学習させているうちに過学習に陥ってしまうケースが大半です。

多項式フィッティングにおける未学習と過学習の例

例えばデータが $\sin$ 関数から生起しているものとして、これがノイズの影響を受けて少しズレた点に生じるとしましょう。

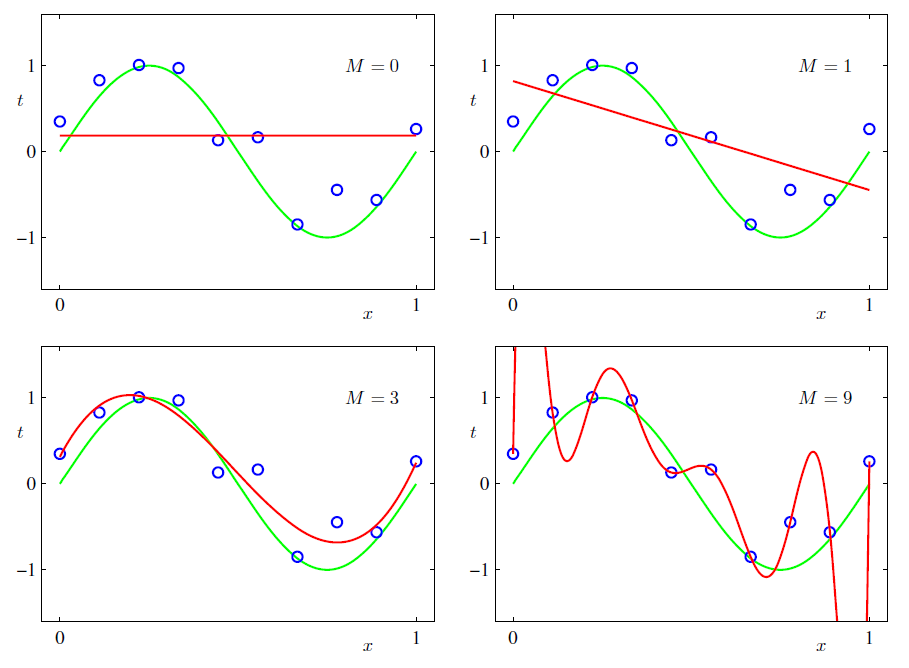
下の図における青い点が、手元の実データです。

緑の線が真のモデル（ $\sin$ 関数)です。

コレに対して赤い線でフィッティングをしようという問題です。

$y=w_0+\sum_{m=1}^{M} w_mx_m$

のような多項式で青い点のデータをフィッティングする場合には、 $M$ の値（つまり多項式の次数）が高いほど複雑な曲線を表現できます。フィッティングの結果が以下の画像です。

$M=0,1$ の場合は完全に未学習と言えます。青いデータ点をほとんど上手く表現できていません。 $M=9$ では、青い点（つまり手元のデータ）すべてを通過する曲線が得られており、訓練誤差だけで言えば非常に優秀です。しかし、この青い点は緑の曲線から生起したものであり、本来のデータの背景を捉えられているとは言えません。新たなデータ点が緑の曲線から生起した時には、そのデータ点を予測するのが困難だというのが分かるでしょう。これが過学習です。

大抵は、モデルを複雑にしさえすれば、訓練誤差を下げることができます。無理やり帳尻合わせができるからです。つまり未学習の解決は容易なのです。

一方で過学習の解決は通常かなり難しいです。まさか $M=3$ がちょうど良いなどということは、最初から知っているわけではありません。何度も学習をして、ちょうど良い値を見つけ出さなければならないのです。

正則化の効力

下記は $L2$ 正則化というものを用いた場合のフィッティングの様子です。

$λ$ は正則化の強さを表す係数で、学習時に適当に設定します。

正則化を導入する場合には、多項式フィッティングでの次数 $M$ の設定は「大きめに」取っておけばよく、過学習しそうな部分を正則化で抑制することができます。大抵 $M$ を調整するより正則化の強さ $λ$ を調整するほうが楽でしょう。

ニューラルネットなどのようにモデルが複雑であればあるほど、正則化に任せる方が考えるべきパラメータを少なくできます。

ここでは、正則化も未学習や過学習を調整するものであるということを納得しておいてください。

評価をするために

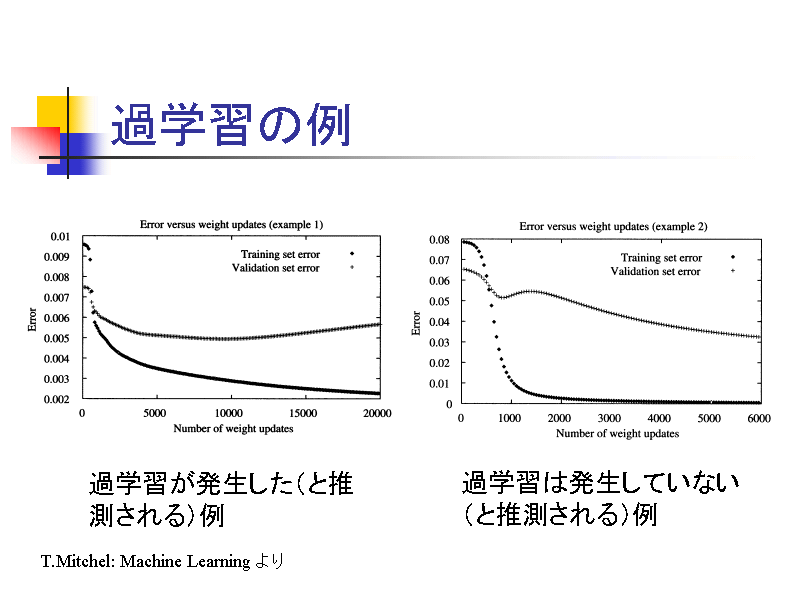
もしも学習をしている最中に過学習に陥っていることに気づけたならば、それ以上学習を進める意味はあまり無いでしょう。それを知るために、機械学習を行う際には訓練データでパラメータを更新するたびに、訓練に用いていないデータを予測するということを行います。

つまり、現段階において予測誤差がどれほどであるのかを逐一チェックするのです。

パラメータが更新されるたびに訓練誤差が下がっていく一方で、予測誤差悪くなっていくのであれば、それ以降は過学習していく傾向があると掴めるわけです。

ここで言う訓練誤差のことを通常は「training error」、予測誤差のことを「validation error」などと言います。大抵の機械学習のライブラリでもvalidationデータを使って、学習中に評価するような仕組みは備わっているはずです。（備わっていなくても作るのは簡単）

（櫻井研究室の講義資料より抜粋）

損失関数の期待値とその分解

バイアス-バリアンス分解は未学習や過学習の状況を理論的に解析する手法です。

これを考えていく上では、まず損失関数の期待値の分解というものを考えなければなりません。

知識的な前提として確率・統計での期待値操作や、テクニカルな面では積分変数の把握ができることが必要となります。

損失関数

訓練データ $\bf x$ に対する正解の値 $t$ がデータとして手元にあるとします。そしてこれからモデル $y({\bf x})$ という関数によって、 $\bf x$ と $t$ の関係を学習させようという設定を考えます。

まず、モデルを学習させる際には損失関数[texL]が必要です。損失関数によって誤差を定義します。ここでは回帰の問題で一般的な二乗誤差を使います。

$L(y( {\bf x} ),t)=(y({\bf x})-t)^2$

これによって、モデル $y({\bf x})$ が正解データ $t$ からどれほどズレてしまっているのかを表現することができます。 $L$ がなるべく小さくなるように $y({\bf x})$ を決定しようというのが学習です。

損失の期待値の最小化

$\bf x$ と $t$ というデータが得られる同時確率を $p({\bf x},t)$ とします。

損失 $L$ の期待値は以下です。

$E[L(y({\bf x}),t) ]=\int \int (y({\bf x})-t)^2 p({\bf x},t)dtd{\bf x}$

機械学習ではこれを最小化するのが目的です。ここで、確率分布の乗法定理によって

$p({\bf x},t)=p(t|{\bf x})p({\bf x})$

とすることができ、これによって積分を

$\int \int (y({\bf x})-t)^2 p({\bf x},t)dtd{\bf x}=\int \left( \int (y({\bf x})-t)^2 p(t|{\bf x})dt \right) p({\bf x})d{\bf x}$

と書き換えることができます。この積分が最小となるためには、括弧の中身（ $dt$ での積分）が最小化されねばならず、このとき機械学習では $y(\bf {x})$ を調整するので

$\frac{\partial}{\partial y({\bf x})} \int (y({\bf x})-t)^2 p(t|{\bf x})dt=0$

を満たさなければなりません。一見難しそうですが、単に $y({\bf x})$ でひとまとまりの変数だと思って偏微分すればよく、

$\frac{\partial}{\partial y({\bf x})} \int (y({\bf x})-t)^2 p(t|{\bf x})dt$

$=2 \int (y({\bf x})-t)p(t|{\bf x})dt$

$=2 \int (y({\bf x})p(t|{\bf x})dt - 2 \int t p(t|{\bf x})dt$

( $y(\bf x)$ は $t$ を含まないので積分の外へ)

$=2 y({\bf x}) \int p(t|{\bf x})dt - 2 \int t p(t|{\bf x})dt$

( $\int p(t|{\bf x})dt=1$ (確率分布は積分したら $1$ ))

$=2 y({\bf x}) - 2 \int t p(t|{\bf x})dt$

これが $0$ となればよく

$2y({\bf x}) - 2\int t p(t|{\bf x})dt = 0$

$⇔$

$y({\bf x}) = \int t p(t|{\bf x})dt = E[t|{\bf x}]$

と求まります。これは回帰問題において $y({\bf x})$ を条件付き期待値 $E[t|{\bf x}]$ で決めると最小化されるということです。

例えば $x = 2$ という値に対して、データ $t$ を集めた場合に、ノイズが生じて $t=4.1$ になったり $t=3.9$ になったりする場合は、きっと $x=2$ に対して $t=4.0$ くらいだろうと見積もることでしょう。

実際の機械学習では、たくさんのいろんな $\bf x_i$ という入力に（例えば入力電圧）対して、得られる正解のデータ $t_i$ （回路の出力電流）があり、その期待値によってモデル（電圧-電流の関係）を構築すると誤差が最小化できるということですが直感的にもそうだと言えますね。

損失の期待値の分解

ここで、理論的な解析を進めるために二乗損失関数の期待値を「具体的に積分計算せずに」、操作を施していきます。二乗損失関数は以下でした。

$L(y( {\bf x} ),t)=(y({\bf x})-t)^2$

これの期待値

$E[L(y( {\bf x} ),t)]=E[(y({\bf x})-t)^2]$

について解析していくということになります。

ここで、変形がテクニカルになるため、丁寧に見て行きましょう。

$(y({\bf x})-t)^2$

に対して、 $-E[t| {\bf x} ] + E[t| {\bf x} ] = 0$ という恒等式を使います。

（引いて足したら $0$ 、当たり前！）

$(y({\bf x})-t)^2 = (y({\bf x}) -E[t| {\bf x} ] + E[t| {\bf x} ] -t)^2$

この変形は当然いつでも成り立ちます。（ $0$ を入れているだけだから）

更に、一見するとテクニカルに見える処理を見やすくするために、以下のように括弧を使って、あたかも $(a+b)^2$ のようにみなせるように書き換えます。

$=\{ (y({\bf x}) -E[t| {\bf x} ]) + (E[t| {\bf x} ] -t) \} ^2$

この状態に対して $(a+b)^2=a^2 + 2ab+b^2$ のように計算を進めることで

$=(y({\bf x}) -E[t| {\bf x} ])^2 +2(y({\bf x}) -E[t| {\bf x} ])(E[t| {\bf x} ] -t) + (E[t| {\bf x} ] -t)^2$

と変形することができます。従って、

$L(y( {\bf x} ),t)=(y({\bf x}) -E[t| {\bf x} ])^2 +2(y({\bf x}) -E[t| {\bf x} ])(E[t| {\bf x} ] -t) + (E[t| {\bf x} ] -t)^2$

であり、この期待値は

$E[ L(y( {\bf x} ),t) ] =E[ (y({\bf x}) -E[t| {\bf x} ])^2 +2(y({\bf x}) -E[t| {\bf x} ])(E[t| {\bf x} ] -t) + (E[t| {\bf x} ] -t)^2 ]$

ですが、実は期待値を取るとこの第二項に関しては $0$ となります（期待値は ${\bf x},t$ に関して積分ですが、第二項はそのときに消えます）。第二項に関して詳しく計算をすると下記のようになります。

$E[2(y({\bf x}) -E[t| {\bf x} ])(E[t| {\bf x} ] -t)]$

$= 2(E[t| {\bf x} ] -t) E[ (y({\bf x}) -E[t| {\bf x} ]) ]$

$= 2(E[t| {\bf x} ] -t) \{E[ y({\bf x})] -E[E[t| {\bf x} ] ] \}$

$= 2(E[t| {\bf x} ] -t) \{E[ y({\bf x})] - E[t| {\bf x} ] \}$

$= 2(E[t| {\bf x} ] -t) \{E[ y({\bf x})] - E[(y({\bf x})] \} = 0$

従って、まとめてしまえば損失関数の期待値 $E[ L(f({\bf x}),t) ]$ は

$E[ L(f({\bf x}),t) ]=E[ (y({\bf x}) -E[t| {\bf x} ])^2 + (E[t| {\bf x} ] -t)^2]$

と表すことができます。

まとめ

損失関数は以下の最小自乗損失を用いる。

$L(y( {\bf x} ),t)=(y({\bf x})-t)^2$

このとき、損失の期待値を最小化するモデルは以下の条件付き期待値となる。

$y({\bf x}) = \int t p(t|{\bf x})dt = E[t|{\bf x}]$

損失の期待値は以下のような2項に分解することが可能である。

$E[ L(y({\bf x}),t) ]=E[ (y({\bf x}) -E[t| {\bf x} ])^2 + (E[t| {\bf x} ] -t)^2]$

バイアス-バリアンス分解

訓練データというパラメータ

損失関数の期待値が

$E[ L(y({\bf x}),t) ]=E[ (y({\bf x}) -E[t| {\bf x} ])^2 + (E[t| {\bf x} ] -t)^2]$

であることを見てきました。

ところが、訓練データの集合 $D=\{ \bf (x_1, y_1),(x_2, y_2),...,(x_n, y_n) \}$ というのは有限です。つまり真のデータのほんの一部を借りてきているに過ぎません。そして、データ１つ１つ $\bf x_i$ を得てくる際には、真のデータからわずかにズレを生じていることでしょう。

そうなってくると当たり前のことですが、これから作るモデルというのは、全く同じ手法を使ったとしても、集めてくる訓練データの集合 $D$ に依存することになります。

したがって、これを明示的に意識するために

$y({\bf x}) →y({\bf x};D)$

$E[t| {\bf x} ]→E[t| {\bf x};D ]$

と書くことにします。

また、損失関数を減少させるようにモデルをフィットさせる時には訓練データ $D$ に対して行っているのであって、

$E_D[ L(f({\bf x};D),t) ]=E_D[ (y({\bf x};D) -E[t| {\bf x} ;D ])^2 + (E[t| {\bf x};D ] -t)^2]$

というように、損失関数の期待値は $D$ に対して計算されることを明示します。

完全なるノイズ項

ここで、完全なるノイズ項を説明しておきます。

以下の式を、期待値計算を項ごとに行うとして

$E_D[ L(f({\bf x};D),t) ]=E_D[ (y({\bf x};D) -E[t| {\bf x} ;D ])^2 + (E[t| {\bf x};D ] -t)^2]$

$=E_D[ (y({\bf x};D) -E[t| {\bf x} ;D ])^2 ] + E_D[ (E[t| {\bf x};D ] -t)^2]$

と分けることにします。このときの第二項に $E_D[ (E[t| {\bf x};D ] -t)^2]$ はノイズ項です。ｌこの項に機械学習で獲得するモデル $y({\bf x};D)$ は含まれていません。

このノイズ項は、機械学習の手法でどれだけ頑張っても、改善することのできない項なのです。

つまり損失関数を低減する上では、この項に成すすべはないということになります。

機械学習で過学習も抑えて、なるべくうまく学習できたと思っても、テストデータの予測性能がどうしても訓練データに見劣りすることがあります。しかしそれは、ある意味仕方のないことでもあるのです。学習は手元に集めたデータのみを考慮しますし、汎用性能を高めようと過学習を抑えてたとしても、ノイズの項は残ってしまうためです。

機械学習では、この第一項の方を考えていくことになります。

バイアス-バリアンス分解

では第一項の方を見て行きましょう。

$E_D[ (y({\bf x};D) -E[t| {\bf x} ;D ])^2 ]$

この式に対して、 $-E_D [y({\bf x};D)]+E_D [y({\bf x};D)]=0$ という恒等式を差し込みます（損失関数を分解したときに使ったのと同じテクニックです）。

$=E_D[ (y({\bf x};D)-E_D [y({\bf x};D)]+E_D [y({\bf x};D)] -E[t| {\bf x} ;D ])^2 ]$

続いて $(a+b)^2=a^2+2ab+b^2$ という計算をするために期待値[texE_D]の中身の項を2つにわけます。

$=E_D[ \{ (y({\bf x};D)-E_D [y({\bf x};D)] \}+ \{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \})^2 ]$

期待値の中身を展開します。

$=E_D[ \{ (y({\bf x};D)-E_D [y({\bf x};D)] \}^2 + \{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \}^2 ...$

$...+ 2\{ (y({\bf x};D)-E_D [y({\bf x};D)] \}\{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \} ]$

これの第3項は期待値 $E_D$ を計算すると $0$ になるので、結局

$E_D[ (y({\bf x};D) -E[t| {\bf x} ;D ])^2 ]$

$=E_D[ \{ (y({\bf x};D)-E_D [y({\bf x};D)] \}^2 ] +E_D [ \{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \}^2 ]$

と計算されることになります。この第一項をバリアンス、第二項をバイアスと言います。

全体としては、損失関数の期待値は

$E_D[ L( y({\bf x};D) ,t) ]$

$= E_D[ \{ (y({\bf x};D)-E_D [y({\bf x};D)] \}^2 ]$ (バリアンス)

$+E_D [ \{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \}^2 ]$ 　(バイアスの（二乗）)

$+E_D[ (E[t| {\bf x};D ] -t)^2]$ 　(ノイズ)

と分解されることになります（バイアス-バリアンス分解）。

バリアンス

$E_D[ \{ (y({\bf x};D)-E_D [y({\bf x};D)] \}^2 ]$

機械学習によるモデル $y({\bf x};D)$ による予測が、訓練データ集合によって変動する度合い（の期待値）を表しており、訓練データに依存し過ぎることで新しいデータへの予測が悪化する度合いを表しています。

言わば過学習に対する指標となります。

バイアス

$+E_D [ \{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \}^2 ]$

機械学習によるモデル $y({\bf x};D)$ が、損失の期待値を最小化する $E[t| {\bf x} ;D ]$ からずれる度合い（の期待値）を表しており、モデルが単純であるあまりに学習が上手くいかない度合いを表しています。

いわば未学習に対する指標となります。

バイアスとバリアンスのトレードオフ

バイアスとバリアンスはトレードオフの関係にあります。

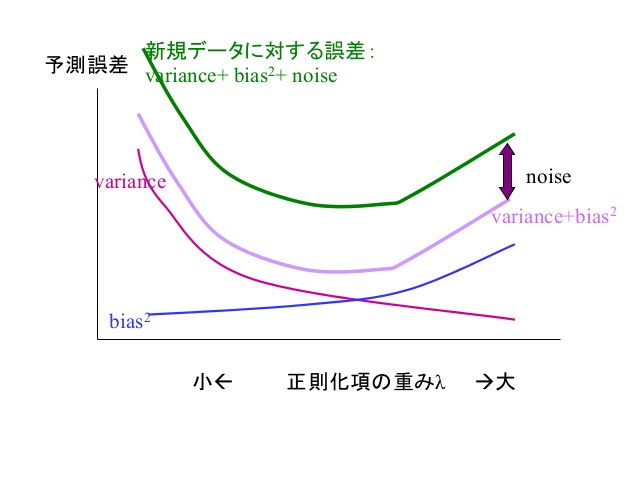
未学習と過学習の関係を考えれば当たり前ですが、これを定量的に評価できることに意味があると言えるでしょう。以下の図を見てください。正則化によって過学習制御を行った場合の、バリアンスのバイアスの関係です。

クラシックな機械学習の入門 4. 学習データと予測性能

過学習制御を小さくしておけば、訓練データに対してはフィットするためバイアスは小さくなります。一方で、データに依存しすぎたあまりに生ずるバリアンスは大きくなります。

過学習制御を大きくすれば、訓練データへの依存度であるバリアンスは小さくなりますが、訓練データにすらフィッティングできなくなりバイアスが上昇します。

損失の期待値は、バリアンスとバイアス（とノイズ）の和であり、バイアスとバリアンスが両方共なるべく低い位置で正則化を決めることで、新規データに対する誤差も小さくなりうるということです。（バイアスとバリアンスの和と、新規データに対する誤差との差がノイズの項で現れる）

もちろん現実では、データがあまり信頼できないならば、バイアスが少々大きくともバリアンスの減少を優先するなどの方法も考えることができます。

全体のまとめ

損失関数の訓練データ $D$ に対する値の期待値を減少させることが機械学習における学習である。その際、訓練データに最適なモデルは

$y({\bf x}) = E_D[t|{\bf x} ;D]$

で与えられる。

しかし、本来の目的は新しいデータへの予測であるため、上記のように完全に訓練データにフィットさせるということはしない（過学習を防ぐ）。

訓練データへのフィットと、新しいデータへの予測ということを考慮したときにバイアス-バリアンス分解というものを考えることができ、損失関数の（訓練データに対する）値の期待値は

$E_D[ L( y({\bf x};D) ,t) ]$

$= E_D[ \{ (y({\bf x};D)-E_D [y({\bf x};D)] \}^2 ]$ (バリアンス)

$+E_D [ \{ E_D [y({\bf x};D)] -E[t| {\bf x} ;D ] \}^2 ]$ 　(バイアスの（二乗）)

$+E_D[ (E[t| {\bf x};D ] -t)^2]$ 　(ノイズ)

で表される。

ノイズは機械学習では対応できない本質的に残留するもの。

バリアンスとバイアスはトレードオフであり、訓練データへのフィットと過学習抑制を同時に考慮する際に、モデルの評価として用いられる。

参考となる書籍

東京大学工学教程情報工学機械学習

作者: 中川裕志,東京大学工学教程編纂委員会
出版社/メーカー: 丸善出版
発売日: 2015/11
メディア: 単行本
この商品を含むブログを見る

パターン認識と機械学習上

作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: 丸善出版
発売日: 2012/04/05
メディア: 単行本（ソフトカバー）
購入: 6人クリック: 33回
この商品を含むブログ (18件) を見る

HELLO CYBERNETICS

深層学習、機械学習、強化学習、信号処理、制御工学、量子計算などをテーマに扱っていきます

バイアス-バリアンス分解：機械学習の性能評価

はじめに

この記事で理解できること

バイアス-バリアンス分解とは

予測性能

未学習とは

過学習とは

多項式フィッティングにおける未学習と過学習の例

正則化の効力

評価をするために

損失関数の期待値とその分解

損失関数

損失の期待値の最小化

損失の期待値の分解

まとめ

バイアス-バリアンス分解

訓練データというパラメータ

完全なるノイズ項

バイアス-バリアンス分解

バリアンス

バイアス

バイアスとバリアンスのトレードオフ

全体のまとめ

参考となる書籍