識別関数、識別モデル、生成モデルの違いを解説

はじめに

記事の目的：共通の認識を持てるようにするため

機械学習が大流行している中で、言葉の定義が曖昧になってきている印象があります。新しい分野が流行すれば、様々なところで言葉が使われ、結果として複数の意味で使われるようになり曖昧になってしまうのは必然です。実際私の周りでも、「ん、どういう意味で使っているんだ？」と思うケースがたまにあります。

ハッキリ言って言葉の意味などは使いやすいように変更されても構わないと思いますし、人間の使い方の統計によって定められていると言っても過言ではないです。

しかし、それでもどの言葉が何を意味しているのかについて共通の認識を持っておくことは大事です。今回は「パターン認識と機械学習」を引用して、識別関数、識別モデル、生成モデルについて解説していきます。

なぜパターン認識と機械学習を引用するか

パターン認識と機械学習は、今や機械学習の古典的名著という位置づけです。更に付け加えるならば、機械学習のベイズ理論による統計的予測について記述したものです。

識別関数、識別モデル、生成モデルという言葉での区別は、統計的な予測という観点に立ち返るとより分かりやすくなります。従って、普通の機械学習手法から統計的な予測という形で解釈しなおし、更にそれをベイズ理論の枠組みで捉え直すという作業を行っている本書では、その違いがハッキリと分かるのです。

パターン認識と機械学習 上

パターン認識と機械学習 下 (ベイズ理論による統計的予測)

機械学習の目的

データがあったときに、そのデータを入力すると、何らかの予測に使える情報を出力してくれる「何か」を構成することが、機械学習の目的です。

分類問題と回帰問題

例えば、画像を入れた時にその画像が猫であるか犬であるかを予測してくれたり、湿度、気温、日にちをまとめたデータを入れたら降水確率を予測してくれたりする「何か」を構成したいという場合に機械学習を使います。

前者は分類問題であって、後者は回帰問題と呼ばれます。これらの決定的な差は、分類問題は「猫」とか「犬」とかなどの明確に違うものを区別するタスクである一方で、回帰問題は数値データに対して数値データを返す点です。

分類問題においては、「猫」とか「犬」という情報の代わりに「０」と「１」と数値を対応させて学習を行うため、結果的には分類問題も数値データに対して数値データを返すことになります。

ただ、ここでの数値というのはあくまで分類を行うための「仮の姿」であるため、学習を行う際には「０」と「１」という数値自体に意味があるわけではありません。「１００」と「５００」でも良いわけで、仮定した設定に応じて学習の方法を考える必要があります。

このあたりは、学習における評価関数（あるいは損失関数）によって調整されることになります。従って、扱う学習機械がニューラルネットワークだろうがサポートベクターマシンだろうが、評価関数の設定次第で回帰にも分類にも対応できます。

分類問題について

回帰というのは非常に分かりやすいです。データを入れたら、それに関連のある何らかのデータの値を出力するというものです。本来の関連性を上手く捉えられていなければ、出力値はまっとうな値からただただ離れていきます。

一方で分類というのは回帰より若干複雑です。３クラス問題において『「馬」、「猫」、「犬」という情報の代わりに「０」、「１」、「２」と数値を対応させて学習を行う』場合に、

1. 「０」と「１」の分類を間違えること
2. 「１」と「２」の分類を間違えること
3. 「２」と「０」の分類を間違えること

は、数値だけを見たら「3.」が一番離れた解答をしているのですが、果たしてそれは真実でしょうか。これは単にクラスの番号付けを人間がそうしているだけであって、学習の出来不出来を左右するものではありません。

このことを踏まえて、「識別関数」、「識別モデル」、「生成モデル」というものを説明していきます。

「識別関数」、「識別モデル」、「生成モデル」

識別関数

識別関数とはデータが入力された際に、そのデータが属するクラスの番号を直接出力する関数のことです。これは機械学習に置いて最も単純な方法であり、問題点として先ほど述べた以下のこと言えることになります。

一方で分類というのは回帰より若干複雑です。３クラス問題において『「馬」、「猫」、「犬」という情報の代わりに「０」、「１」、「２」と数値を対応させて学習を行う』場合に、

1. 「０」と「１」の分類を間違えること
2. 「１」と「２」の分類を間違えること
3. 「２」と「０」の分類を間違えること

は、数値だけを見たら「3.」が一番離れた解答をしているのですが、果たしてそれは真実でしょうか。これは単にクラスの番号付けを人間がそうしているだけであって、学習の出来不出来を左右するものではありません。

要するに分類がどのように間違っているのかを知るすべが無いということです。

また、入力データの次元がならば、次元空間上に識別超平面を直接構築することになりますが、識別超平面からデータがどれくらい離れているから「良い」だとか「悪い」だとかの評価すら困難であるということになります。

サポートベクターマシンは識別関数の部類です。

データ空間上に識別超平面を構築しますが、その際には、分類が際どいデータのみを上手く選んで、それらと識別超平面がなるべく離れるように学習を行います。

s0sem0y.hatenablog.com

s0sem0y.hatenablog.com

識別モデル

識別モデルではデータがクラスに属する確率をモデル化します。つまり３クラス分類においては、クラスに属するデータが入力されたならば

などとなるようなを構成しようということです。この場合は、正しいクラスの確率が大きくなるように学習できていれば、学習が上手く言っていると言えますし、分類が上手く言っていたとしても

などとなるようでは、クラス１と分類はできても、学習が怪しそうだということが言えます。更に、どのクラスと間違ってしまいがちであるかも分かります。このような場合には、例えば単に確率が高いクラスを選ぶのではなく、確率が60%以上になった場合にのみ判定をするなど、決定の方式を準備しておくことで二段構えにしておきます。（識別関数では確率に基づいた二段構えができない）

このようにデータに対するクラスの条件付き確率（事後確率）をモデル化するのが識別モデルです。

ソフトマックス交差エントロピーを使ったニューラルネットワークはこの識別モデルに相当します。ニューラルネットワークの出力層は上記で述べたとおり、各クラスに属している確率を出力しており、通常は、最も値の高いクラスを選択するようになっています。

s0sem0y.hatenablog.com

生成モデル

生成モデルでも同様にをモデル化することを考えますが、その方法が違います。この事後分布をベイズの定理によって以下のように表記し直します。

実際に求めるのは右辺の方です。分類をしたいだけなら新たなデータがに対して右辺を計算した後に、識別モデル同様何らかの方法でクラスを決定すればいい話です。

生成モデルはそれだけでなく、右辺そのものを何かに応用することができる点にあります。このときは、クラスに対するデータの条件付き分布になっています。これを求めることができた時には、例えばのクラスに属するデータがどんなものであるかを知ることができたということです。

分母に関してはなる分布によって入力に人工的なデータを作り出すことができます。モデルからデータを創りだしたり、あるいは言わば、というクラスのデータをサンプリングすることが可能であるということです。

これが生成モデルと呼ばれる所以です。データを入れたらクラスを分類してくれるだけでなく、使い方によっては、あるクラスに属する擬似的なデータそのものを作ることができるのです。

基本的にベイズモデルは総じて生成モデルです。

最も数学的に複雑な扱いが必要であり、実際に学習の段階に持っていくためには様々な近時操作も必要になってくるケースが多いです。

また分母を求めることができた場合には、（このモデルのもとで）データがどれくらいの割合で存在するのかを知ることができたということになります。低い確率で現れるデータ点に対する分類精度は低いと考えられます。一方で、低い確率で存在する「外れ値」や「新規性」データの検出にも用いることができます。

ナイーブベイズモデルが代表的な生成モデルです。

最近画像認識で流行りのGANなども生成モデルだと言われています。なぜなら、擬似的なデータをサンプリングできるように構成されているからです。現状はサンプリングさえできれば生成モデルということで意見が一致しているように思います（必ずしもベイズの定理の形式を完全に近似しなくても構わなさそう）。

生成モデルのメリットデメリット

データをサンプリングできる、新規性や外れ値の検出ができるなど、データそのものについて最も吟味できることが生成モデルの最大のメリットであります。一方で、数学的な操作が面倒である点など、お気楽に使えないというデメリットもあります。

しかし、実を言うと必ずしも生成モデルのほうが分類精度が良いとは限りません。まず訓練データが多数必要です。そうでないとこれほど詳細なモデル化はできません（識別関数であるサポートベクターマシンは本当に少数のデータでも使えます）。また、

において、右辺のはサンプリングに使えても、さほど分類の確率には影響しません。従って、分類だけが目的なら識別モデルでも何ら問題はないのです。

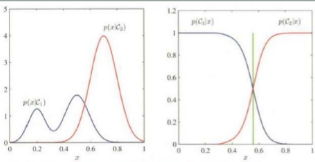
左はを、右はを図示している。

赤と青がそれぞれのクラスの確率を表している。

左は青のクラスのデータが多峰性を持つことを示してくれているが、青と赤が明らかに左と右に分かれているため、分類には影響が出ていない。

深層生成モデル面白そうだけど、私の分野ではどうも必要なさそうだ。機会があれば勉強してみたい。

以下の東大松尾研究室の輪講資料に結構深層生成モデルがあります。

deeplearning.jp