はじめに
最近はGoogle/Jaxに興味を持ってしまっており、その上にあるNumPyroが確率プログラミングとしてもかなり有用そうである…という思いが強くある状態でした。NumPyroとはPyTorch上に構築された確率プログラミングライブラリPyroをJaxのnumpy上に構築したライブラリです。
numpyroの最大の利点は、jax.jitをNUTSのアルゴリズム高速化にフル活用しており、圧倒的にMCMCサンプリングが速いことです。もはやPyroの上位互換か…と思っていたところなのですが、実際私はJaxの関数型のパラダイムに不慣れで、以前PyTorchの方が使いやすいと感じている状態です。
そこでふと、Pyroに再び戻って見ると、あいも変わらずMCMCは遅い…ということが確認できたのですが、MCMCには目もくれずに変分推論周りのモジュールや時系列モデリング周りが進化していたのです。もうそちら方向に特化すると決めているのだなという雰囲気を感じます。 そこで、超進化していた(気づかなかっただけで結構前からあった?)時系列モデリングのモジュールを紹介します。
Pyroで時系列モデリング
モジュールのインポート
import math import torch import pyro import pyro.distributions as dist import pyro.poutine as poutine from pyro.contrib.examples.bart import load_bart_od from pyro.contrib.forecast import ForecastingModel, Forecaster, eval_crps, backtest from pyro.infer.reparam import LinearHMMReparam, StableReparam, SymmetricStableReparam, LocScaleReparam from pyro.ops.tensor_utils import periodic_cumsum, periodic_repeat, periodic_features from pyro.ops.stats import quantile import matplotlib.pyplot as plt plt.style.use("seaborn") pyro.enable_validation(True) pyro.set_rng_seed(20200305)
なんだかインポートが膨大ですが、pyro.infer.reparam や pyro.ops.tensor_utils 、そして pyro.contrib.forecast に時系列を便利に扱うすばらしいものが用意されていました。
データ
Exampleにもある公共交通機関の利用者データを一時間毎に取得したものです。 一ヶ月分のデータ(24 hour × 30 days)を可視化します。
dataset = load_bart_od() print(dataset.keys()) print(dataset["counts"].shape) print(" ".join(dataset["stations"])) data = dataset["counts"].sum([-1, -2]).unsqueeze(-1).log1p() plt.figure(figsize=(9, 3)) plt.plot(data) plt.title("Total hourly ridership over one month") plt.ylabel("log(# rides)") plt.xlabel("Hour after 2011-01-01") plt.xlim(len(data) - 24 * 30, len(data));
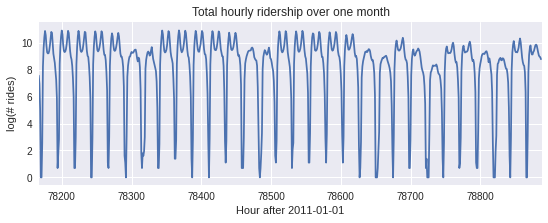
土日は公共交通機関の利用者が少なくなるかもしれません。
ひとまず訓練データとテストデータを分離しておき、 訓練データの一週間ごとの平均的推移を見てみましょう。 これは重要な特徴として使えるかもしれません。
T0 = 0 # beginning T2 = data.size(-2) # end T1 = T2 - 24 * 7 * 2 # train/test split means = data[:T1 // (24 * 7) * 24 * 7].reshape(-1, 24 * 7).mean(0) plt.plot(means)

時系列モデルの書き方
pyro.contrib.forecastにあるForecastingModelクラスを継承して実装します。
実装しなければならないのは model(self, zero_data, covariates) というメソッドになります。
model メソッドは戻り値はなくても良くて、内部で self.predict(noise_dist, prediction) が "一度だけ" 呼ばれる形で書けばよいです。これは観測モデルを書くことに相当します。書くために noise_dist と prediction が必要なので、modelメソッド内部でnoise_dist と prediction を定義しておく必要があります。
下記では noise_dist を定義するために get_dist メソッドを分離しています。
class Model(ForecastingModel): ## 観測モデルの分布を書く。GaussianHMMに必要なパラメタに事前分布を準備。 ## ノイズは周期的に変化することを織り込む def get_dist(self, duration): init_dist = dist.Normal(0, 10).expand([1]).to_event(1) timescale = pyro.sample("timescale", dist.LogNormal(math.log(24), 1)) trans_matrix = torch.exp(-1 / timescale)[..., None, None] trans_scale = pyro.sample("trans_scale", dist.LogNormal(-0.5 * math.log(24), 1)) trans_dist = dist.Normal(0, trans_scale.unsqueeze(-1)).to_event(1) obs_matrix = torch.tensor([[1.]]) with pyro.plate("hour_of_week", 24 * 7, dim=-1): obs_scale = pyro.sample("obs_scale", dist.LogNormal(-2, 1)) obs_scale = periodic_repeat(obs_scale, duration, dim=-1) obs_dist = dist.Normal(0, obs_scale.unsqueeze(-1)).to_event(1) noise_dist = dist.GaussianHMM( init_dist, trans_matrix, trans_dist, obs_matrix, obs_dist, duration=duration) return noise_dist ## zero_data のshapeの後ろから2番目がdurationという決まりである。 ## prediction は一週間ごとの平均を使う。 ## HMMをnoise_distに利用しているので covariates は使われない。 def model(self, zero_data, covariates): duration = zero_data.size(-2) prediction = periodic_repeat(means, duration, dim=-1).unsqueeze(-1) noise_dist = self.get_dist(duration) self.predict(noise_dist, prediction)
試しに、GHMMの事前分布から100時間の系列データをサンプリングしてみましょう。
model = Model() prior_sample = model.get_dist(T2-T1+24*7)([100]) p10, p50, p90 = quantile(prior_sample, (0.1, 0.5, 0.9)).squeeze(-1) plt.plot(torch.arange(T2-T1+24*7), p50) plt.fill_between(torch.arange(T2-T1+24*7), p10, p90, alpha=0.3)

とくに意味のない系列データになっております。
学習
学習は非常にシンプルに書けます。上記で書いたモデルクラスのインスタンスと、観測データと共変量(HMMなので不要)を準備し、学習率とエポック数を指定してForecaster クラスに渡してあげます。戻り値は学習が終了済の予測推論ができるようになっているインスタンスです(なんか凄い設計だな…)。
%%time pyro.set_rng_seed(1) pyro.clear_param_store() covariates = torch.zeros(len(data), 0) # empty forecaster = Forecaster(model, data[:T1], covariates[:T1], learning_rate=0.1, num_steps=1000) for name, value in forecaster.guide.median().items(): if value.numel() == 1: print("{} = {:0.4g}".format(name, value.item()))
検証(バックテスト)
複数のモデルを検討する場合にはバックテストで汎化性能の評価をしておかなければなりません。 与えたデータを自動で時系列を考慮して分割を行い、バックテストを実施してくれる関数があります。
観測データと共変量、あとは"モデルクラス"(インスタンスではない。なぜなら、バックテスト内部で、train valid のデータ毎にインスタンスを再生成し直して評価しなければならないから)を与えます。また、学習に使う最小の時間窓と未来予測検証に使う時間窓、そして検証をする上ではずらす時間窓の大きさをそれぞれ指定します。
%%time pyro.set_rng_seed(1) pyro.clear_param_store() windows1 = backtest(data, covariates, Model, min_train_window=20000, test_window=10000, stride=5000, forecaster_options={"learning_rate": 0.1, "log_every": 1000, "warm_start": True})
ここで、上記の関数は、
D_train = D[0:20000] D_test = D[20000:25000]
での検証から開始し、
D_ train = D[0:25000] D_test = D[25000:30000]
と次の検証に移ります。したがって k 番目の検証では
D_train = D[0: min_train_window + (k-1) * stride] D_test = D[min_train_window + (k-1) * stride : min_train_window + (k-1) * stride + test_window]
というデータの使い方をします。すると、今後のtest_window分の未来予測をする際に、訓練データが単調に増加していく形式での検証となります。(すなわち過去に取得できているデータは溜め込んで、常に学習に使っていくということ)
他のやり方としては、訓練データ側の窓は大きくせずにスライドしていく方法もあります(すなわち過去のデータは捨てて行き、常に固定の量の訓練データしか使わないということ)。
※ これらの長所短所・あるいは理論的背景を私は認識できていません。どなたかご存知であれば…。 感覚としては、前者のテストは訓練サイズが増えていく(過去のデータが溜まっていく)毎にモデルを再学習すれば、テスト性能が良くなることを確認できると思われるので、継続的に使えるモデルの選択に使えるのかなと思います。後者は、今の手持ちのデータだけで今後の将来を予測するモデルを選択するときの指標(すなわちある固定のデータ量を使って将来予測をしたときの汎化性能の統計量を評価)になるかなと思います。なんとなく後者が最も素直な気がしますが、Pyroは前者の方法のようです。
コンソールには下記の出力が出てきます。
INFO Training on window [0:20000], testing on window [20000:30000] INFO step 0 loss = 0.994833 INFO step 1000 loss = -0.00330511 INFO Training on window [0:25000], testing on window [25000:35000] INFO step 0 loss = 0.141774 INFO step 1000 loss = 0.0935524 INFO Training on window [0:30000], testing on window [30000:40000] INFO step 0 loss = 0.101058 INFO step 1000 loss = 0.0781855 INFO Training on window [0:35000], testing on window [35000:45000] INFO step 0 loss = 0.0591136 INFO step 1000 loss = 0.0530795 INFO Training on window [0:40000], testing on window [40000:50000] INFO step 0 loss = 0.0264387 INFO step 1000 loss = 0.0224656 INFO Training on window [0:45000], testing on window [45000:55000] INFO step 0 loss = 0.0111767 INFO step 1000 loss = 0.00672334 INFO Training on window [0:50000], testing on window [50000:60000] INFO step 0 loss = -0.0191512 INFO step 1000 loss = -0.0209487 INFO Training on window [0:55000], testing on window [55000:65000] INFO step 0 loss = -0.0362959 INFO step 1000 loss = -0.037423 INFO Training on window [0:60000], testing on window [60000:70000] INFO step 0 loss = -0.0515607 INFO step 1000 loss = -0.0534813 INFO Training on window [0:65000], testing on window [65000:75000] INFO step 0 loss = -0.0598117 INFO step 1000 loss = -0.060701 CPU times: user 10min 24s, sys: 2.82 s, total: 10min 27s Wall time: 10min 28s
予測
forecaster の __call__ が、そのまま予測を実施するメソッドになっているため、データと共変量とサンプルサイズを渡してあげます。信用区間を得る関数も準備されているので簡単に可視化の準備ができます。
samples = forecaster(data[:T1], covariates, num_samples=100) samples.clamp_(min=0) # apply domain knowledge: the samples must be positive p10, p50, p90 = quantile(samples, (0.1, 0.5, 0.9)).squeeze(-1) crps = eval_crps(samples, data[T1:]) plt.figure(figsize=(10, 5), dpi=100) plt.fill_between(torch.arange(T1, T2), p10, p90, color="red", alpha=0.3) plt.plot(torch.arange(T1, T2), p50, 'r-', label='forecast') plt.plot(torch.arange(T1 - 24 * 7, T2), data[T1 - 24 * 7: T2], 'k-', label='truth') plt.title("Total hourly ridership (CRPS = {:0.3g})".format(crps)) plt.ylabel("log(# rides)") plt.xlabel("Hour after 2011-01-01") plt.xlim(T1 - 24 * 2, T1 + 24 * 4) plt.legend(loc="best");

実はHMCも対応しているので、MCMC版とVI版でバックテストを回して見ようかと思ったのですが、Jit使うとエラーが出る上に、Jit外すと、1サンプルを得るのに9秒かかるという始末だったので、諦めました(1000サンプル得るのに9000秒…2時間〜3時間くらいね)。