はじめに
台車型の倒立振子でのシステム方程式は所与とし、これに対してLQRを用いて制御をする例を示します。 コード例はMATLABを用います。
LQRによる制御
制御対象の状態空間モデル
まず制御対象の状態空間モデルは $$ \dot x = A x + B u $$ と与えられているとします。また観測方程式は $$ y = Cx + Du $$ です。台車式倒立振子の方程式は、倒立が成功している状態の近傍にて下記のように表されます。本来は非線形方程式ですが、今回は線形化することでLQRを用いていきます。
$$ \begin{align} A _ {23} &= -\frac{3mg}{4M+m} \\ A _ {43} &= \frac{6(M+m)g}{4Ml+ml} \\ A &= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & A _ {23} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & A _ {43} & 0 \end{bmatrix} \\ B _ 2 &= \frac{4}{4M+m} \\ B _ 4 &= -\frac{6}{4Ml+ml}\\ B &= \begin{bmatrix} 0 \\ B _ 2 \\ 0 \\ B _ 4 \end{bmatrix} \\ C &= \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ D &= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix} \end{align} $$
上記の数式に関しては下記の記事を参考にしています。
台車型倒立振子を安定にフィードバック制御する|Tajima Robotics
LQR
LQR(Linear Quadratic Regulator)は線形システムの最適制御設計において広く使用される手法の一つです。通常、フィードバック制御では安定性や追従性などを考慮した極配置を実施し、フィードバック則を導出します。一方で最適制御では、目標値と制御入力に対して理想的な振る舞いを指定したコスト関数を導入し、最適化問題として解くことでフィードバック則を得ます。LQRはその一例ということになります。
まず、線形システムを次のように表します。
$$ \begin{equation} \dot{x}(t) = Ax(t) + Bu(t) \end{equation} $$
LQRのコスト関数は、以下の式で表されます。 $$ J = \int _ {0}^{\infty} [x ^ T(t)Qx(t) + u ^ T(t)Ru(t)] dt $$ ここで、$Q$は状態重み行列、$R$は入力重み行列です。LQRではシステムが線形(Linear)であり、コスト関数が二次(Quadratic)であることが要件となります。
ここで、状態 $x$ を観測できるとすると、制御則は以下の式で表されます。 $$ u(t) = -Kx(t) $$ ここで、$K$は状態フィードバックゲイン行列です。このゲインをオフラインで求めることで制御を実施することになります。 このゲインはコスト関数を最小化するような値になるよう設計され、下記のリカッティ方程式を解くことで得られます。 $$ A ^ T P + PA - PBR ^ {-1}B ^ T P + Q = 0 $$ ここで、上記を満たす$P$は、リカッティ方程式によって決定される状態フィードバックゲイン行列 $K$ とすることができます。
LQRのコード例
まずは下記のようにパラメータを設定します。
% 倒立振子の物理的パラメータ M = 1.0; % カートの質量 [kg] m = 0.1; % 振子の質量 [kg] l = 0.5; % 振子の長さ [m] g = 9.81; % 重力加速度 [m/s^2] A23 = -3*m*g/(4*M+m); A43 = 6*(M+m)*g/(4*M*l+m*l); A = [0 1 0 0; 0 0 A23 0;0 0 0 1; 0 0 A43 0]; B2 = 4/(4*M+m); B4 = -6/(4*M*l+m*l); B = [0;B2;0;B4]; C = eye(4); D = zeros(4, 1);
次に下記のコードでLQRの設計が可能です。
% 最適レギュレータの設計 Q = diag([1, 0.1, 10, 0.1]); R = 0.1; [K, S, E] = lqr(A, B, Q, R); % K がフィードバックゲイン行列
これを用いて、状態の時間発展をシミュレートします。
% シミュレーションの設定 Tf = 10; % シミュレーション時間 [s] Ts = 0.05; % サンプリング時間 [s] T = 0:Ts:Tf; % シミュレーションの時間軸 N = length(T); % シミュレーションの時間ステップ数 % 参照信号の定義 x_ref = zeros(4, N); % x_ref(1, :) = 2*sin(2*pi*T); % 初期状態の定義 x0 = [0; 0; pi/4; 0]; % 制御入力の初期化 u = zeros(1, N-1); f = @(x, u) A*x + B*u; % シミュレーションの実行 x = zeros(4, N); x(:, 1) = x0; for k = 1:N-1 % 現在の状態と参照信号の取得 xk = x(:, k); x_ref_k = x_ref(:, k); % 状態フィードバックによる制御入力の計算 u(k) = -K*(xk - x_ref_k); % シミュレーションの実行 x(:, k+1) = xk + f(xk, u(k))*Ts; end
これにより下記のように参照信号に対して状態が収束しているのが確認できます。
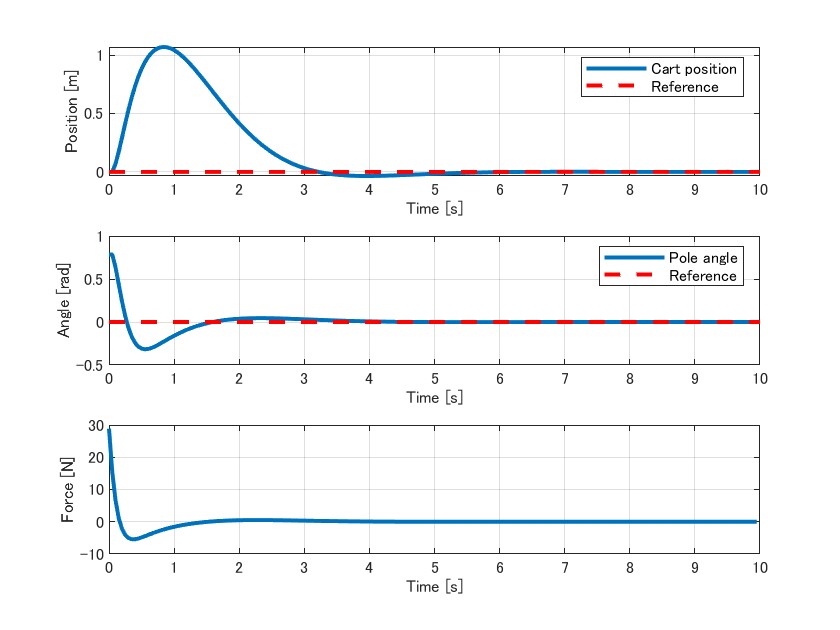
簡易的に倒立振子の振る舞いを描画しておきます。
% アニメーションの描画 figure; axis_limit = 2; % カートと振子の表示範囲 x = x'; for i = 1:T_steps cla; cart_x = x(i, 1); pendulum_x = cart_x + l * sin(x(i, 3)); pendulum_y = l * cos(x(i, 3)); plot([cart_x, pendulum_x], [0, pendulum_y], '-', 'LineWidth', 2); hold on; yline(0, "LineWidth", 2) plot(cart_x, 0, 'ks', 'LineWidth', 2, 'MarkerSize', 20); hold off; xlim([-axis_limit, axis_limit]); ylim([-axis_limit, axis_limit]); xlabel('x [m]'); ylabel('y [m]'); title('Inverted Pendulum Animation'); drawnow; end

未知の外乱が生じる場合
最適制御では制御則導出の時点でシステムの方程式を知っているということが重要です。一方で実際の制御時には、想定していなかった外部からの力が加わったりなどが考えられます。 今回は、カートに取り付けられている振子がふらついており、勝手に外力が加わってしまうという例で制御がどうなってしまうのかを確認します。 状態の時間発展を少し修正します。
d = 0.3*sin(2*pi*0.5*T) + randn(1,N); Bd = [0;0;1;0]; f = @(x, u, d) A*x + B*u + Bd*d; % シミュレーションの実行 x = zeros(4, N); x(:, 1) = x0; for k = 1:N-1 % 現在の状態と参照信号の取得 xk = x(:, k); x_ref_k = x_ref(:, k); % 状態フィードバックによる制御入力の計算 u(k) = -K*(xk - x_ref_k); % シミュレーションの実行 x(:, k+1) = xk + f(xk, u(k), d(k))*Ts; end
フィードバック則は当然外乱が加わったことを知りませんし、外乱がない場合に最適な動作をするということしかできません。したがって倒立振子は外乱の影響をもろに受けて、その分揺らいでいるのが分かります。

最後に
外乱オブザーバーを用いると、既知のシステムに対して生じている外乱を推定することができます。 これを用いて制御則を修正することで制御を改善することができる可能性があります。外乱オブザーバーの例については下記を参考にしてみてください。
また、強化学習でCartPoleはExampleとして頻出ですが、この程度の系ですら直接的な制御を上手に実施するための学習コストは非常に高いことが知られています。問題の抽象度が高く、不確定性が高い、かつ制御性に対する許容度が高い場合には有効かもしれませんが、堅実な制御の手法も知っておくと多くの場面で活躍するでしょう。