
ディープラーニングを手軽に始められるようにはなったものの、実際に学習を上手く進めるにはチューニングという作業が欠かせません。ここではチューニングの際に気をつけることをサラっとまとめておきます。
層の数とユニットの数
層の数
層が多いことの弊害
ディープラーニングの恩恵を受けたい場合には、層は基本的に3層以上にします。しかし層が多いほど学習の可能性は広がるのですが、良い結果が得られるとは限りません。
層の数が増えるほど学習は難しくなります。ニューラルネットの学習は、誤差逆伝搬法によって行われますが、誤差逆伝搬法の性質上、層が増えるほど正しく誤差を伝搬していくことが困難になるためです。
本来は、学習させるタスクによって、どのような関数が仮定される(べき)かは変わってきます。しかしニューラルネットを用いる場合は、本来必要とされる関数よりも明らかに複雑なものを準備しておいて、学習によって必要な関数の形まで近似します。
従って、過度に層を増やして複雑にしすぎてしまうと、近似を進めていく段階で局所的な解や鞍点につかまりやすくなってしまうというわけです。あるいは過学習を起こす可能性も否定できません。
また、当然ですが層が増える毎に計算量が増えていくことも、実用上留意しておく必要があります。
基本的指針
タスクの複雑さに応じて層の数は調整する必要があるのですが、多くの場合は、層の数を適当に多めに取って学習をさせます。もちろん、最初は間違いなく過学習を起こしてしまいます。そこで過学習の調整は、ドロップアウトや正則化などのテクニックを使って対応することになります。
発展的方法
仮に層少なくしても学習ができるのならばそちらのほうが都合が良いのは間違いありません。色々な他のパラメータを弄りながら、学習を何度も行って調整を繰り返さなければならないディープラーニングにおいては、1回1回の学習が早く済むのは明らかなメリットです。
そこで、層の多いニューラルネットで、与えられたタスクの達成が可能であると分かれば、そのニューラルネットの出力と同じものを出せるように、もっと層の少ないニューラルネットを学習させる「蒸留」と呼ばれる手法もあります。
正則化を行う場合、最適化の目的関数は、交差エントロピーなどの損失関数に加えて、正則化項
が付与され以下のようになります。
理想的な学習が行われた段階(学習が収束→勾配がの状態)に置いては
となっているはずであり、これを暗黙知識といいます。
層の多いニューラルネットが学習を終えた段階では、この暗黙知識を獲得したを保持しているはずです。そこで蒸留では、学習を終えた層の多いニューラルネットの出力を「ソフトターゲット」と呼び、実際の教師データを「ハードターゲット」と呼んで、両方を、より層の少ない学習に用います。
ここでソフトターゲットには、層の多いニューラルネットが正則化なども考慮して学んできたために、ハードターゲットにはない過学習を防ぐ情報が含まれれていることが期待できます。
ユニットの数
前提の知識
学習は、入力に対して、教師ラベル
を出力してくれるような関数
をつくり上げることです。関数
として、
が
に近づくように
を調整することになります。
このとしてニューラルネットを用いるのが、ニューラルネットの学習ですが、中間層1つあれば、そのユニット数を任意に変えることで連続関数を自在に表現できることが知られています。
しかしこれから表現したい関数というものがいかなるものであるのかを我々は知りません。従って、「任意のユニット数」もどうすればいいのかが分かりません。
学習の指針の例:情報圧縮
ユニットの数に関しても、明確に定められる方法はありません。
ディープラーニングに期待することの1つとしては、「なんだかよくわからないが特徴量を自分で見つけてくれること」が挙げられるでしょう。そうともあれば、ニューラルネットを用いる際には、手元のデータに対して特徴量が明確に分かっておらず、整理されていない状況を想定するはずです。
もしもニューラルネットへの入力データの次元がかなり大きくて、これから達成するタスクに対して情報過多であることが見込まれるならば、中間層の数は減らしたほうが良いと考えられます。
ニューラルネットが次元の大きな情報から、タスクに必要な小さな次元の情報を取り出してくれることを期待するからです。しかし、それでもどれくらいの層を準備すれば良いのかは定かではありません。
仮に本来タスクに必要な次元よりも、小さな次元になるようにユニットの数を設定してしまった場合には、ニューラルネットは本来必要だった情報を一部捨てなければならないことになります。従って、結局のところ必要なユニット数がわからない以上、恐らく必要だと思われるユニット数よりも多めに取っておくことが必要になります。
ここでもニューラルネットの過学習を助長することになってしまいます。このようなケースにもドロップアウトや正則化などを上手く使うことによって対応することになります。
本来L1やL2正則化は、次元を多く摂り過ぎた場合の、上手い選択の指針を学習に組み込むために生まれたものです。従って、正則化項を調整することは、ユニット数を多めに取っておいた場合の学習にクリティカルに響いてきます。また、ユニット数を変えれば、正則化項の重み付けについても考慮し直す必要があるということになります。
ニューラルネットの中間層の役割
出力と入力の架け橋
ニューラルネットの出力層は、分類ではソフトマックス関数を、回帰では線形関数を用います。これらはそれぞれ比較的簡単な処理であり、従ってこの出力層だけでは複雑なタスクをこなせないことが多いです。
そこで中間層は最終的な出力を行う出力層に対して、扱いやすく都合の良いデータを提供するように学習が行われます。簡単なデータしか扱えない出力層と、複雑なデータとの架け橋の役割をしているのです。
どのような架け橋を学習できるか、その複雑さや柔軟性が層の数やユニットの数で決まってきます。
中間層による表現力の柔軟性
単層パーセプトロンでは排他的論理和すら学習できないことが知られています。これはニューラルネットを学ぼうと思った人は一度は聞いたことがあるでしょう。これは、単層パーセプトロンでは排他的論理和という関数を表現できないためです。これが多層化をすることで解決されることもよく知られている事実です。
中間層が増えることによって、ニューラルネットが表現できる関数が増えます。
これからニューラルネットに行わせたいタスク(関数)を、ニューラルネットが表現できるように準備されていなければならないのです。

正則化
分類タスクにおける損失関数には交差エントロピー、回帰のタスクには二乗誤差が用いられます。しかし実際の学習ではこれらの損失関数に、正則化項を加えることが多いです。
与えられたタスクに対する損失関数をとして、正則化項を
とすると
という形をしています。正則化項は本来の損失関数に比べて、それほど重要ではないケースが多いので、通常は小さな定数(例えば
)などを係数として掛けます。
これらの正則化について見ていきましょう。
L1正則化
L1正則化の概要
L1正則化とは、
に関して、
と設定することです。「」がなるべく小さな値となるためには、
も小さな値でなければならず、結果として
の各要素がなるべく
になるように学習が行われます。
L1正則化の役割
例えば入力層が3つのユニットで、その次の中間層も3つのユニットだったとしましょう。中間層のとある1つのユニットへの入力に着目します。

この図のように入力層の各ユニットの値にがそれぞれ乗じた状態で、次のユニットに入力が行われます。ここにL1正則化を用いると、
はなるべく
になるように学習が進むため、入力される値が制限されることになります。すなわち、与えられたタスクに必要な入力を自動で見つけてくるようになるのです。タスクに不要なユニットに値には、重み
が付与されるようになり、無効化されます。
ハイパーパラメータ の調整
の調整
上記のように、L1正則化では入力される値を選びとるという性質が得られることが分かりました。その場合、例えば入力されるデータが既に「全て必要なデータである」と分かっている時にこの正則化を入れる意義はあまりありません。あまりにもデータの次元が大きく、必要なデータもそうでないものも混じっている場合には有効に働くことでしょう。
一方で、中間層と中間層の間に正則化を入れることも考えられます。基本的にニューラルネットは、与えられたタスクに対して、明らかに複雑な関数として置かれています。L1正則化では与えすぎた複雑さを学習の中で減少させることに一役買うというわけです。
従って、ハイパーパラメータは仮定したニューラルネットの複雑さとタスクの難易度、データの次元に応じて設定されなければなりません。
L2正則化
L2正則化の概要
L2正則化とは、
に関して、
と設定することです。「」がなるべく小さな値となるためには、
も小さな値でなければならず、結果として
をベクトルと見た時に、このベクトルが大きくなり過ぎないように学習が行われます。
L2正則化の役割
再びニューラルネットの一部に着目してみましょう。
入力のとき、次の層のあるユニットには下図のように
が入力されます(はバイアス)。

この入力の式は、としておけば、以下のように内積を使って表現できます。
内積とはベクトルとベクトルからスカラー値を得る計算です。スカラー値の大きさは、ベクトルとベクトルの方向性の違いや、ベクトル自身の大きさに依存します。にどのような方向性と大きさを持たせるかは学習で決まっていきます。

このことを考えると、仮にというベクトルが好きなようにやたらめったら大きくなれた場合には、次の層への入力を、自在にやたらめったら大きくできてしまうことになります。方向性に関しては通常、特に制限をする必要はないでしょう。どのような変換が良いのかわからないからこそ学習させるわけですから。
通常、好き勝手に入力値の大きさをによって調整できてしまうと過学習を引き起こします。
なぜならば、明らかにおかしな外れ値(やけに大きな値など)にも対応できるようになってしまうためです。本質的でないデータには対応しないことが学習には求められるため、あえて学習に制限を掛ける役割を担っています。
正則化がもたらすニューラルネットへの影響
正則化がもたらすニューラルネットへの影響を、図で直感的に把握しましょう。この話はニューラルネットでなくとも通用する重要な概念です。
正則化が上手に働く状況
下記の図を見てください。登場するのは
- ニューラルネットが表現できる関数の範囲
- ニューラルネットが正則化の制限化で表現できる関数
- 真の関数
- 質の良い学習データ
- 室の悪い学習データ
です。
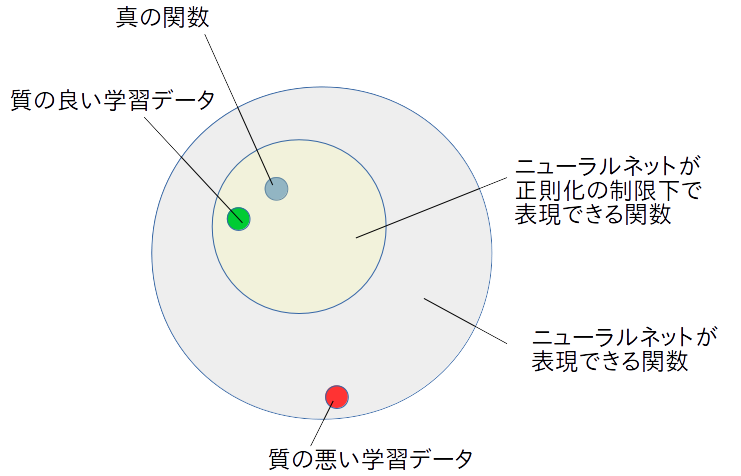
ニューラルネットはを学習で調整することによって、表現できる関数内のどれかに落ち着きます。ニューラルネットの構成次第で、この表現できる関数の範囲は変わります。
今ニューラルネットに達成させたいタスクに対応する理想の関数が真の関数です。この真の関数の姿を私達は知りませんが、学習データを使ってニューラルネットに見つけさせたいという状況です。
この図の状況の場合、正則化を用いなかった場合、質の悪い学習データに対応した挙句、真の関数とは程遠い何かに、ニューラルネットが収束してしまう可能性があります。
しかし、正則化によって上手くニューラルネットの表現できる関数を制限できれば、質の悪い学習データに引きづられる可能性を防ぐことができます。
学習データには質の良いデータも悪いデータも混じっていることでしょう。上手く正則化を働かせることで、質の良いデータばかりであり、そのデータが完全に真の関数を導くに値するのであれば、正則化なんてものは必要がありません。
しかし、現実にはそうはいかず、多かれ少なかれノイズなどを含んでしまうことが多々あるのです。過学習とは、言わばタスクとは本質的に関係のないデータに引きずられ、それを学習してしまうことです。
一部のデータがそもそも必要のないものであるのか、全て必要なのだがノイズが乗ってしまっているのか、状況によりけりでしょう。上手くL1正則化とL2正則化を使いこなして、ニューラルネットの学習をコントロールしましょう。
正則化が失敗する例
今度は正則化が上手く働かない例を見ます。
以下の図を見れば明らかです。
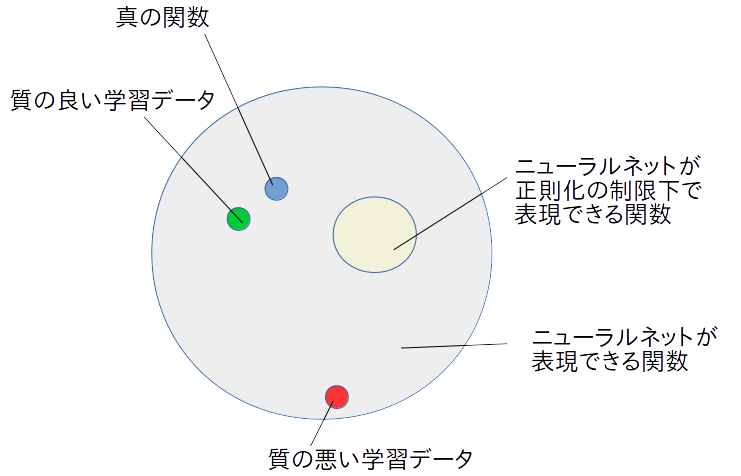
正則化によって、ニューラルネットの表現できる範囲を極度に制限してしまったため、全く持って真の関数に近づくことができなくなっています。通常、この状態を未学習と言います。
単層パーセプトロンが排他的論理和を表現できないのと同じように、正則化を強くしすぎたニューラルネットは、本来こなしたいタスクを全くこなせなくなる可能性があることを認識しなければなりません。
正則化における方針
最初は過学習でも良いので、正則化は弱めにしておくことから始めて、まずニューラルネットが望んだタスクをこなせる表現力を有しているのかを確認する必要があります。
そして過学習を防ぐために後から、正則化を強めていくというのが妥当な方針でしょう。
最適化法
学習における偽物の解
仮にニューラルネットの設計や、正則化が上手く働いていても、かならずしも学習結果が良くなるとは限りません。ニューラルネットは基本的に勾配法と呼ばれる方法で、損失関数を減少させる方向に少しずつ進んでいきます。しかし、学習の開始地点から、本来到達したい地点まで、損失関数が綺麗に減少していくとは限りません。

ニューラルネットがを少しずつ調整しながら、学習データを表現できるように学習を進めていくのですが、進んでいく過程に、その周りよりは損失関数が小さくなる地点が存在し、そこにハマってしまうのです。
これは最適化の分野でも大きな課題です。通常損失関数が、凸関数でない限りは綺麗に収束することは保証できないのです。
また、通常ニューラルネットには多くの鞍点が存在します。
勾配法は損失関数が小さくなる方へ進むのですが、小さくなる方を調べるために勾配を計算します。しかし、鞍点においてはすぐ隣に小さくなる地点があるのですが、勾配がになってしまうため、身動きが取れなくなります。
いわば、局所解や鞍点というのは勾配法にとっては偽物の解として振る舞うのです。
ニューラルネットに置いては局所解に行くことはそれほど問題ではないかもしれません。なぜなら目的であるタスクを達成できるのであれば、本来関数の形はどのようなものであっても構わないからです。従って、一番の問題は鞍点ということになってきます。なにせ、ちょっと頑張ればもっと良くなることは分かっている地点であるからです。
ちなみにニューラルネットには鞍点がアホほど存在します。
改良された勾配法
勾配法では鞍点を効率よく抜け出すことができません。
そのため
- モメンタム法
- AdaGrad
- RMSProp
- Adam
などの手法が提案されてきました。
ニューラルネットを使う際に、最適化方法が色々あって迷う、あるいはよくわからないという人も多いと思いますが、基本的にこれらは、鞍点を抜け出すことを考えた手法であると思って構いません。
ちなみに、どれが一番かなんてことを決めることはできません。
極端な話、鞍点なんてものが存在しない場合においてはAdamが学習を邪魔する可能性だってあります。すなわち、あるタスクでAdamが良かったからって、ほかのタスクでも良いとは限らないということです。
なぜなら、タスクに応じて、あるいは同じタスクでも学習データの質によって損失関数は形を変えるためです。当然ニューラルネットの構成によっても損失関数は変わります。一般に損失関数はニューラルネットの構成、入力データ、教師データに依存しますし、いろいろな損失関数に対して万能な最適化法など存在しません(ノーフリーランチ定理)。
ただ、ノーフリーランチ定理は全ての可能な損失関数に、最適化法を試していった場合に、その平均的性能は同じになるという話です。
ニューラルネットの学習という限られた損失関数の中に置いては、ある最適化法が、ある複数の限られたタスクにおいて有効であると判明することはありえます。
大抵の場合はAdamは上手く働きます(もちろん他が良い時もありますが)。
従って、良くわからんかったらAdamを使ってみるのが良いでしょう。
(ハッキリ言って、ニューラルネットは最適化という観点においては力任せで適当な感じなので、もう色々試してみるしか無いというところ)
ドロップアウト
ドロップアウトは、学習に参加させるユニットを制限する手法です。学習の最中に、ドロップアウトしてしまうユニットを交代していくことで、一種のアンサンブル学習を行うことができます。
また、ユニットの数を制限しているという点に置いて、過学習を防ぐことにも繋がります。
アンサンブル学習
アンサンブル学習の考え
アンサンブル学習は簡単に言えば、複数の判定器を使って最終判定を行うように学習する方法です。
1つの判定器は、タスクに対して万能である必要はなく、例えば10クラス分類において、1〜3のクラスの分類は得意であるように学習されても良いのです。そのような性能がちょっと低いが、互いを補い合える「弱学習器」を寄せ集める方法がアンサンブル学習の基本的考えです。
ドロップアウトとアンサンブル学習
ドロップアウトでは、ある3クラス分類の学習においては以下のユニットの選択をするかもしれません。以下のようにドロップアウトしてしまうユニットを決めたら、残ったユニットだけで構成されたニューラルネットを使うことで、とりあえず学習をします。

元々のニューラルネットよりもユニット数が少ないので、基本的に性能は落ちてしまうことが予測できますが、その一方で過学習抑制にも繋がります。また出力層は通常ドロップアウトしません。各クラスである確率を表す層であるためです。
その後再びドロップアウトするユニットを選び直し、学習を続けます。

今度は先ほどと違う構成のニューラルネットを学習することになります。
このようにドロップアウトするユニットを変えていくことで、いろいろなパターンのニューラルネットを学習させることになります。
実際にテストデータを分類させる際には、全てのユニットを用いることに注意してください。すなわちこれまでバラバラに選ばれて学習していた、いろいろなパターンのニューラルネットの意見を集大成して分類するということになります。
ドロップアウトをした場合の学習について注意点
学習を進めながら、テストデータに対する性能を確かめることをした場合には、学習データに対するAccuracyよりも、テストデータに対するAccuracyの方が高くなる場合があります。
それは、学習データに対してはドロップアウトをしており、テストデータには全てのユニットを使って分類をしているためです。驚いてしまう人がたまにいますが、上記のドロップアウトの事情を考えれば納得がいくところでしょう。
最後に
ディープラーニングでは学習を上手く進めるための様々な工夫があります。それ故に、どの工夫がどれだけ聞いてくるのかを把握することは非常に難しいです。何度も学習を試しながら、良い方法は何なのかを試行錯誤する必要があります。
GPUの必要性・使われ方
ディープラーニングは学習に時間がかかります。それだけでなく、ハイパーパラメータの調整で何度も学習し直すことになるでしょう。従ってGPUはディープラーニングに必須の道具と言えます。
例えば、GPUを4つ積んだ場合には、各GPUにハイパーパラメータを変えた4パターンのニューラルネットを別々に学習させて、比較するという使われ方がします(1つのGPUに、もっとぶち込めるならそうすればいいです)。
場合によっては1つのニューラルネットを高速に学習させるために、学習の並列計算が行われる場合もありますが、まだ適したニューラルネットを探している最中であれば、前者の使い方の方が適しているでしょう。
色々なニューラルネット
ニューラルネットの学習に関しては、一般的な考え方を述べてきましたが、タスクに応じてネットワークの構成そのものを変更する必要が出てくる場合もあります。
以下の畳み込みニューラルネットと、LSTMについては是非抑えておきましょう。
ニューラルネットの学習で何が起きてるか
今回はニューラルネットを関数と見立てて、最適化という視点から話をしました。以下では分類問題において、ニューラルネットが中間層で何を学習しているのかについて述べています。
中間層で何を学習しているのかを把握すると、ニューラルネットの転移学習に関する意義も理解できるようになるでしょう。
転移学習については以下の外部の記事を参考にしてください。